The Two Sides of Isaac Newton

It is well-known that Isaac Newton invented the calculus, and that his laws of motion and gravitation launched mathematical physics. Some brilliant British physicists carried on the tradition; think of Hamilton, Maxwell, Kelvin* et al. But where were the mathematicians? The answer is: across the English Channel. Leibniz had also invented the calculus, and engaged in a vicious dispute with Newton over priority (Bardi 2006). Newton’s followers went off in the huff, and took British mathematics into a wilderness where it stayed, give or take, for 150 years.

The problem for British mathematicians was that Newton and Leibniz had invented the same calculus, but radically different notations — and notation really does matter! Newton denoted derivatives by dots, for example \(\dot x\) and \(\ddot x\), and called them ‘fluxions’. Leibniz denoted derivatives by \(dx/dt\), \(d^2x/dt^2\) and so on, and in due course we came to call them ... well, ‘derivatives’. Leibniz’s \(dt\) notation also made the connection between derivatives and integrals \(\int x\ dt\) much more transparent, and proved adaptable to multiple dimensions and variational calculus. Leibniz's superior notation was shunned in Britain, but adopted by continental analysts such as Euler and the Bernoullis, whose legacy then flourished with Lagrange, Abel, Jacobi and Gauss through Cauchy, Riemann, Weierstrass et al. to Hilbert, Poincaré, Lebesgue and Borel et al. at the turn of the 20th century.  Bell (1953) is still an entertaining if sometimes romanticized account.

Meanwhile in Britain:

• One of Newton’s successors as Lucasian Professor, Robert Woodhouse (1820–22), campaigned with little success to wean his colleagues off fluxions. (He resigned the position because it was so poorly paid.) (O’Connor & Robertson 2005).

• Our own Benjamin Gompertz remained loyal to Newton and fluxions all his life. He wrote in (Gompertz 1862) about his dislike of “the furtive notation used on the Continent and now much used in England”.**

• Not until the 20th century did G.H. Hardy drag the notorious Mathematical Tripos at Cambridge out of the shadow cast by Newton, saying it had “effectively ruined serious mathematics in England for a hundred years” (Snow 1967). (Hardy was perhaps the first British analyst of the front rank since Maclaurin. His analysis was largely self-taught from works in French.)

Many things shaped the nascent UK actuarial profession (Turnbull 2017), but we should not overlook the isolation of British mathematics, and the moribund state of the universities. On the plus side, and speaking relatively, Britain was politically stable, open to commercial enterprise, and had a growing middle class with wealth (and female relatives) to protect. From these roots the profession emerged to meet a need, then evolved quite apart from the universities, even after these recovered their place in the intellectual life of the nation. Nor were actuaries alone:

the professional tag was so sought after that the rush to respectabilize was unstoppable. By the end of the century, architects, accountants and engineers had all created their own professional institutions

Paxman (1991 p.106)

Fast-forward 100 years, and we see Frank Redington, the outstanding British actuary of his age, writing a famous paper including inter alia his theory of immunization (Redington, 1952). With hindsight, it might seem that he was equipped with the wrong (nonstochastic) calculus; Newtonian in spirit if not notation. However, it would be silly to suggest that Redington, an actuary working in the senior echelons of an insurance company, should have known about a stochastic calculus still confined to research journals. Recall the actual genesis of stochastic ‘immunization’, as far as Black & Scholes (1973) breakthrough two decades after Redington’s paper. Economists trained in US universities (heirs to Humboldt’s vision of the research university) connected an old Parisian thesis (Bachelier (1900), examined by Poincaré no less) with a Japanese paper on stochastic analysis (Itô, 1944) directly descended from Lebesgue and Borel (France again) via Kolmogorov (Russian), and married everything up with recent non-arbitrage ideas.

Figure 1 below gives an impression of the great calculus split, the early stage at which Britain entrusted actuarial matters including mathematics to a professional body, and what went on in the Leibnizian branch of history.

Figure1. The Great Calculus Split and the UK actuarial profession. blue = theory, red = application.

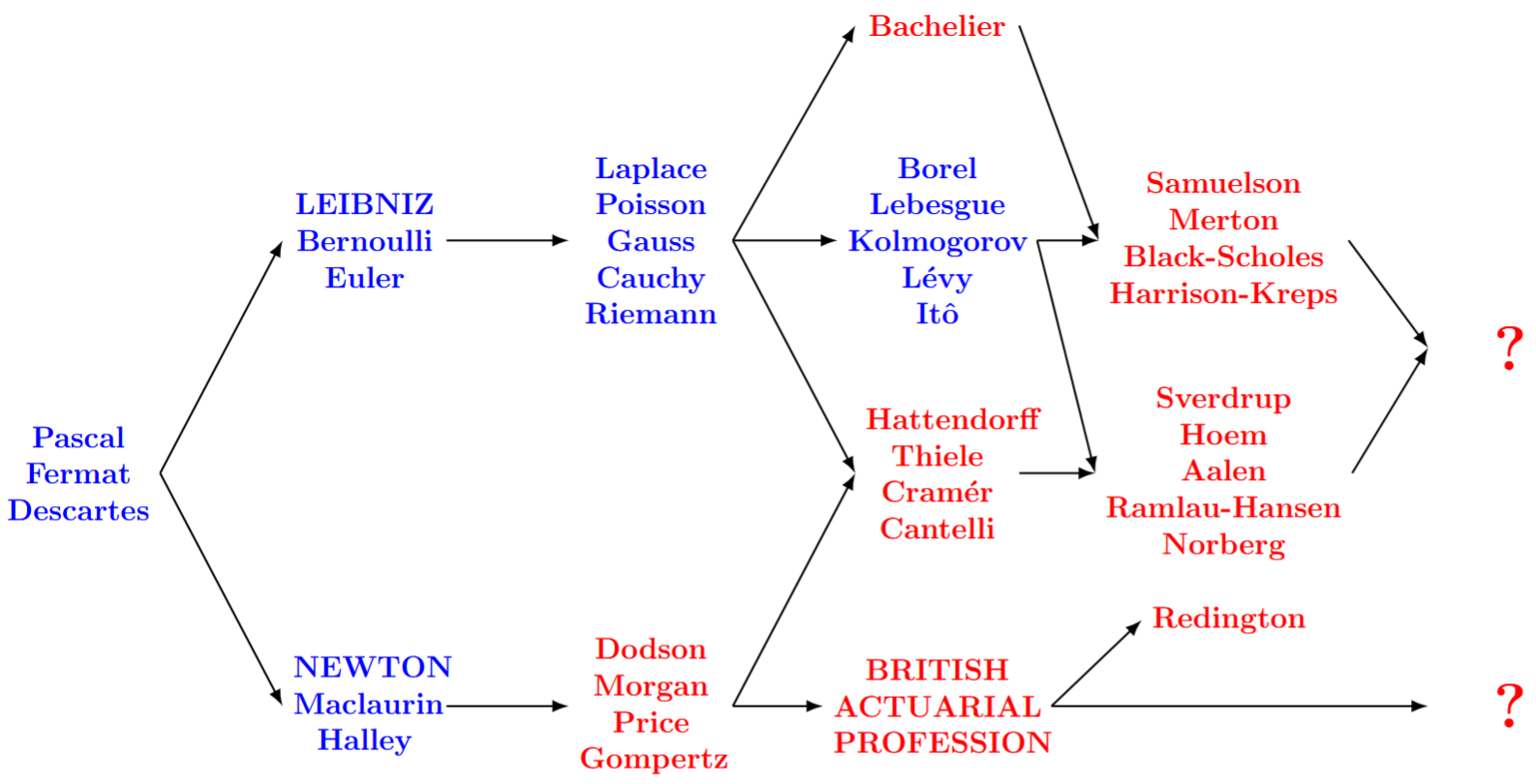
There is much more in Figure 1 than this short blog can explore, so just two final remarks:

• The Scandinavian influence on modelling biometric risk, including survival models, is shown in the node headed by Sverdrup, and has featured in several of these blogs.

• Figure 1 highlights mathematics and there is more to actuarial science than mathematics. Therefore the lower (Newtonian) branch looks unfairly bare. It is interesting to contrast how Redington (1952) was received by actuaries concerned with large-scale institutional funds (see discussions preserved in JIA and TFA), and the immediate adoption of the Black-Scholes formula by traders in options exchanges (Mackenzie 2006).

Footnotes:

* Respectively Irish working in Ireland, Scottish working in England and (Northern) Irish working in Scotland.

** In fairness, Gompertz’s dislike was based on genuine doubts about infinitesimals, shared by others, though these doubts were cleared up by Cauchy before Gompertz’s death.