The enduring need for deduplication

In Macdonald et al (2018, Section 2.5) we describe the importance of deduplication, i.e. the identification of individuals behind multiple policies.  This is a critical step for a statistical model, as lives can be regarded as independent, whereas the mortality experience of two or more policies written on the same life clearly are not.

Deduplication has a long history in actuarial investigations.  Downes (1862) described the creation of a card-index system for an experience investigation. A card was created for each policy, containing the name and date of birth of the policyholder, together with the exposure period.  The cards were then sorted and individuals with multiple policies identified; a single substitute card was then created that amalgamated the exposure periods for the various policies.  Thus, a series of overlapping policy exposures in Figure 1 would become the single life exposure period in Figure 2.

Figure 1.  Three policies written on the same life.  Source: Downes (1862, page 14).

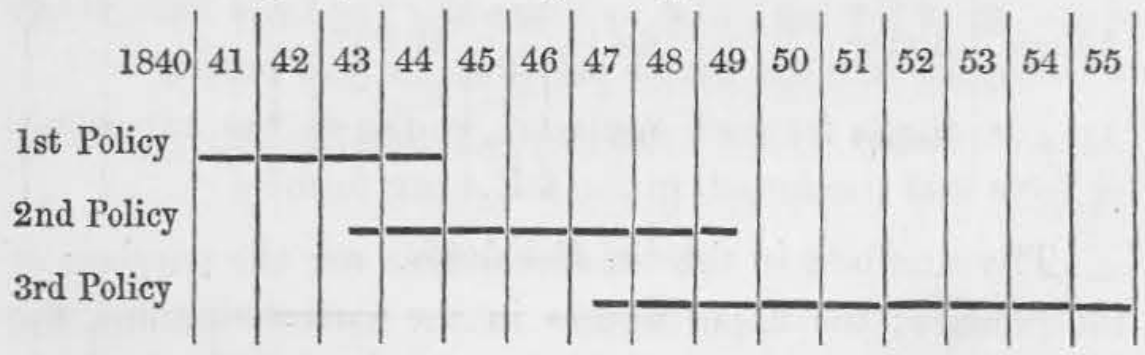
Figure 2.  Single substitute exposure record created from the three policies in Figure 1.  Source: Downes (1862, page 14).

Downes (1862) employed a combination key to identify duplicates, i.e. where adjacent cards had the following matching data items:

1. Surname

2. Forename

3. Date of birth

Using this approach, Downes (1862, page 19) identified 9,335 lives covered by 11,945 life-insurance policies, i.e. an average of 1.28 policies per person.  By way of comparison, we found an average of 1.24 policies per life in the annuity portfolio in Richards and Currie (2009, page 320).  That's two different classes of business separated by 150 years, and yet the same phenomenon is common to both.  As long as insurers and pension schemes have policy- and benefit-orientated administration records, actuaries will need to deduplicate for their experience investigations.