An early bath for the bathtub model
My last posting looked at why actuaries fitted survival models differently to statisticians, even though the conceptual framework for survival models is common to both disciplines. In this posting we look at why actuaries and demographers use different models from engineers.
Survival analysis plays an important role in reliability engineering, and survival models are used to model the time to failure of a component or device. Mathematically this is the same as modelling the time to death of an individual, although engineers use different terminology from actuaries and demographers. However, although the mathematics is identical, the shape of the hazard function is typically very different: mechanical and electrical components often have a high initial failure rate which decreases for a while, and then gradually increases with age. This pattern is known as a bathtub hazard model. This is a stark contrast to the mortality of adult humans, which typically increases steadily with age.
This difference in the shape and behaviour of the hazard function leads actuaries and engineers to require very different types of survival model. By way of illustration, Figure 1 shows the fitted mortality rates under two models for the experience data of a medium-sized pension scheme in the UK. It is clear that the "actuarial" model is a far better fit than the "bathtub" model. This does not invalidate the bathtub model in an absolute sense, it merely says it is not useful for mortality work. We are likely to find exactly the reverse situation if we were to model the lifetime of, say, light bulbs in a quality-control setting. In each case, the choice of hazard function depends critically on its suitability for the risk being modelled.
Figure 1. Log(mortality) for a medium-sized UK pension scheme, together with the fitted rates according to the Perks law of mortality and the Hjorth "bathtub" model. Source: Own calculations.
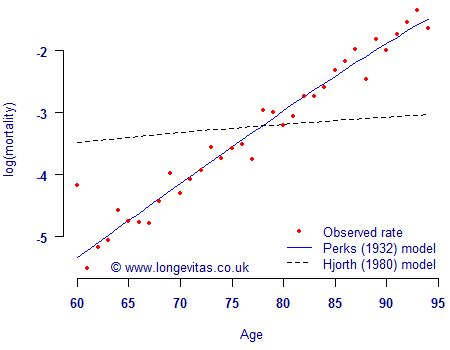
There is a huge choice of possible survival models, but only a small number are likely to be relevant to a particular application. Figure 1 shows that bathtub-style hazards for reliability studies are inappropriate for modelling pensioner mortality. Actuaries and others concerned with adult mortality — and longevity in particular — will choose the models most applicable to this risk.
Previous posts
Actuarial exceptionalism
In an earlier posting I listed some actuarial terms and their statistical equivalents (and later a short list of statistical terms and their equivalents in other fields). Using different expressions for the same concept is an unfortunate barrier to understanding across disciplines.


Add new comment