Significantly enhancing your models
In building a mortality model (or any other kind of risk model) it is usually best to build a single, over-arching model rather than split the data into sub-groups (an approach called stratification, the disadvantages of which are discussed in Macdonald et al (2018)). One obvious reason is to reduce the total number of parameters: why fit two parameters for age when one will do? Another reason is that a larger data set will have more power and thus smaller standard errors. In the example discussed here we merge the data sets of two pension schemes to gain more statistical power when measuring shared risk factors such as age and gender.
However, a less obvious reason not to stratify is that the single model can lead to the discovery of significant risk factors that might otherwise remain hidden. Consider Figure 1, which shows the parameter estimates and their significance levels for a variety of risk factors:
- age,
- whether a pensioner is male (Gender.M),
- whether a pensioner retired early (EarlyLate.Early),
- whether a pensioner has medium-sized pension (HighSize.2) or a particularly large pension (HighSize.3). and
- whether the pensioner belongs to the second of the two pension schemes (Scheme.2).
Figure 1. Parameter estimates and significance levels before enhancement. Source: Longevitas Ltd. *** denotes significance at the 0.1% level, ** at 1%, * at 5% and . at 10% level.
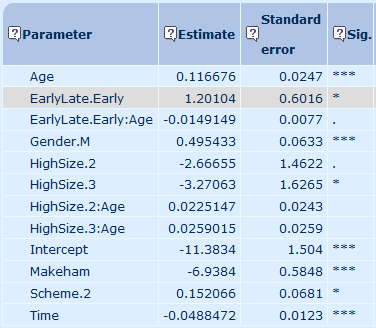
In Figure 1 we see that two of the parameters are only weakly significant, as denoted by the '.':
- the main effect of being in the medium pension-size group (HighSize.2), and
- the interaction with age of the effect of retiring early (EarlyLate.Early:Age).
Now compare these results with the equivalently named parameters in Figure 2, which is the same model but where we now allow the effect of scheme membership (Scheme.2) to vary with age by adding an interaction (Scheme.2:Age). Both of the weakly significant parameters in Figure 1 have suddenly become much more significant. Indeed, several of the already-significant parameters have become even more so, such as the parameter for the effect of pension scheme (Scheme.2).
Figure 2. Parameter estimates and significance levels after enhancement. Source: Longevitas Ltd.
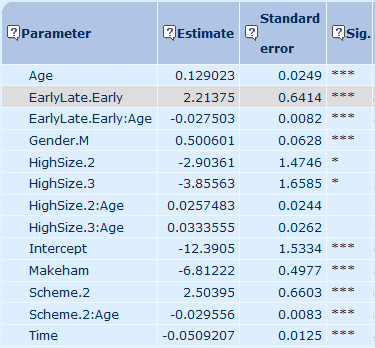
This is an example of enhancement — adding a new parameter can improve the ability of existing parameters to explain mortality variation. Enhancement is not rare. Indeed, in the words of Currie and Korabinski (1984):
"We found that enhancement was extremely common [...] as a stepwise regression proceeds [...], so enhancement becomes more frequent."
Source: Currie and Korabinksi (1984).
One can think of enhancement as a virtuous circle. It is also a reason to re-test risk factors that were not initially promising, in case their importance is masked by another factor (a phenomenon called concealment). What Currie & Korabinski noted more than three decades ago remains true for models today.
References:
Currie, I. D. and Korabinski, A. (1984) Some comments on bivariate regression, The Statistician 33 283–293.
Macdonald, A. S., Richards. S. J. and Currie, I. D. (2018). Modelling Mortality with Actuarial Applications, Cambridge University Press, Cambridge.


Add new comment