Forecasting with penalty functions - Part III
This is the last of my three blogs on forecasting with penalties. I discussed the 1-d case in the first blog and the 2-d case in the second. Here we discuss some of the properties of 2-d forecasting. Some readers may find some of my remarks surprising, even paradoxical.
In our first blog we used the Lee-Carter model as an example where a time series is used to forecast mortality. The method is (a) estimate the parameters in the model by fitting the model to suitable data and (b) forecast a subset of the parameters with a suitable time series. The fit to data, by definition, does not depend on the forecast horizon. This is a familiar and attractive property; we will refer to this as the invariance property. It is easy to overlook the fact that a price has been paid for this invariance: we use distinct processes in the data and forecast region, ie, there is a discontinuity between the model used in the data region and the method used to forecast.
Forecasting with penalties is a seamless method, by which we mean fitting and forecasting are done simultaneously; the model both fits and forecasts. We have avoided the discontinuity referred to in the previous paragraph, but as a consequence there is no reason a priori that the invariance property should hold. Nevertheless, in 1-d we saw that the invariance property does hold. However, it does NOT hold in 2-d, and the purpose of this blog is to explain (a) why it cannot hold and (b) why we should be quite relaxed about this.
Let us suppose for the moment that we are wedded to the idea of invariance. We saw in my blog on 2-d modelling that we should think of our regression coefficients as arranged on a grid. The blog on 1-d modelling and forecasting then tells us that we will achieve invariance if we perform 1-d forecasting on each row of coefficients; this will produce linear forecasts at each age. It is straightforward to write down the penalty matrix that achieves this, and Figure 1 shows the results; we call this penalty the invariant penalty. We have used Australian male mortality data for ages 50 to 90, and years 1960 to 2010; the forecast is to 2060. The result is not acceptable. The crossing of the forecasts for ages 50 and 60 occurs in 2057. It is easy to see why this has occurred. There is a flattening of the age 50 mortality from 2000 to 2010; the 2-d model, as a local model, is sensitive to this flattening and picks it up. The forecast at age 50 reflects this local behaviour.
Figure 1: Observed, fitted and forecast mortality for Australian males with the invariant penalty.
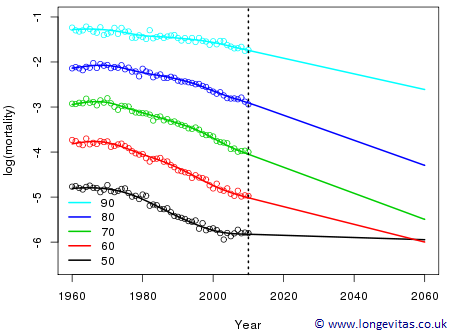
The invariant penalty has many attractive properties.
- The fitted values in the data region are invariant with respect to the forecast horizon.
- Forecast values to 2030, say, are invariant with respect to any forecast horizon greater than 2030.
- The effective dimension, the deviance and the smoothing parameters are invariant with respect to the forecast horizon and equal to the values found when fitting to data only.
The problem with Figure 1 is that there is nothing in the invariant penalty to control the forecasts across ages. We need a penalty which (a) forecasts and (b) preserves the structure across ages; this is precisely what the 2-d penalty achieves (Currie, Durban and Eilers, 2004). The forecasts at ages 50 and 60 will be kept apart and a balance is struck between forecasting in time and preserving the structure across ages.
None of the "attractive properties" listed above holds. Some readers may find this disconcerting. Most, maybe even all, other methods of forecasting fit to data and then use a time series to forecast: invariance becomes the conventional wisdom. However, with 2-d methods a single surface is fitted over the entire data and forecast region. The penalty sets up a tension across the whole surface with the result that the forecast affects the fit in the data region; it is a kind of feedback mechanism familiar throughout the natural world. Figure 2 shows the fit and forecast with the 2-d penalty. Everything has turned out well.
Figure 2: Observed, fitted and forecast mortality for Australian males with the original 2-d penalty.
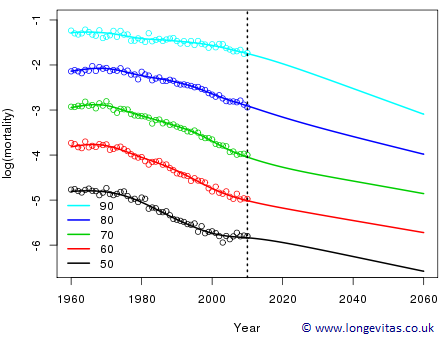
Table 1 compares the forecasts for 10, 25 and 50 years. Although we no longer have exact invariance we have what we might call statistical invariance, by which we mean that all differences are not statistically significant, in the sense that all BIC values are very similar (recall that two models whose BIC values are less than four units aparts are not significantly different). The final column is probably of most interest to actuaries. Let \(\hat {\boldsymbol{\Lambda}}\) denote the table of fitted log mortalities when there is no forecasting and let \(\hat {\boldsymbol{\Lambda}}_F\) denote the corresponding table when forecasting is to year \(F,\, F = 2020, 2035, 2060\). The final column of Table 1 gives values of \(\max(\mbox{abs}((\hat {\boldsymbol{\Lambda}}_F - \hat {\boldsymbol{\Lambda}})/\hat {\boldsymbol{\Lambda}})) \times 100\); these differences are very small indeed.
Table 1: Smoothing parameters, \(\lambda_a\) and \(\lambda_y\), effective dimension, ED, Bayesian Information Criterion, BIC, and %-differences for various forecast horizons.
| Forecast horizon, \(F\) | \(\lambda_a\) | \(\lambda_y\) | ED | Dev | BIC | % difference |
|---|---|---|---|---|---|---|
| 2010 | 94.9 | 546.1 | 55.2 | 4272.4 | 4694.6 | \(-\) |
| 2020 | 91.5 | 558.5 | 54.9 | 4274.2 | 4693.6 | 0.07 |
| 2035 | 86.1 | 577.5 | 54.8 | 4275.5 | 4694.2 | 0.16 |
| 2060 | 87.3 | 570.4 | 54.8 | 4275.5 | 4694.4 | 0.18 |
To sum up: 2-d forecasting may only be statistically invariant but this is a small price to pay for a single minimum tension surface across the whole of the data and forecast region. As W. S. Gilbert remarked in The Pirates of Penzance: it is a most ingenious paradox!
Acknowledgement: I am very grateful to Maria Durban, Carlos III University, Madrid, and Dae-Jin Lee, Basque Center for Applied Mathematics, Bilbao, for drawing my attention to their work on the invariant penalty.
References:
Currie, Durban & Eilers (2004). Smoothing and forecasting mortality rates, Statistical Modelling, 4, 279–298.
Human Mortality Database. University of California, Berkeley, USA. Available at www.mortality.org (data downloaded 2015).


Add new comment