Rise and fall of causes of death
When projecting mortality rates it is common for people to ask what sort of changes in causes of death might be required to achieve a particular scenario. Often one is asked to posit what causes of death have to be "eliminated", and the results can lead to the conclusion that a particular projection is unlikely and therefore too prudent.
However, this is sometimes due to forgetting that reducing mortality due to one cause of death can increase the rates of mortality due to another. One example is prostate cancer, which was historically considered rare but by 2008 had become the fifth most common cause of death amongst males above age 85 in England and Wales (and the most common cancer cause of death, beating even lung cancer). Mortality rates for this age group are shown in Figure 1.
Figure 1. Mortality rates per 10,000 males over age 85 in England & Wales. Source: 20th Century Mortality.
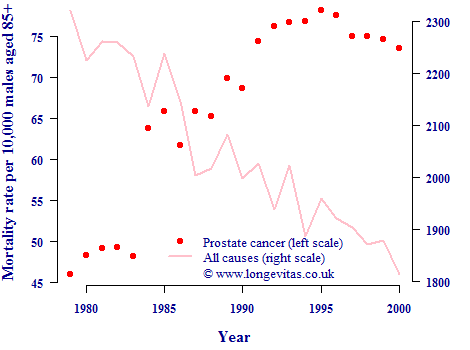
Although all-cause mortality rates in this age group have fallen steadily, the mortality rate due to prostate cancer has clearly risen. Prostate cancer is slow-growing, and it is often described as something a male is more likely to die with than from. As other causes of death reduced, however, the likelihood of dying from this cause actually increased. Unless this sort of linkage is allowed for, using cause-of-death "elimination" calculations make scenarios appear more prudent than they are. Such calculations are sometimes used to communicate mortality projections, but this example shows that this could lead to a false level of comfort.
On a final note, there is a clear discontinuity in prostate-cancer mortality rates between 1983 and 1984, which is suggestive of a change in diagnosis and/or classification. This serves to underline the uncertainty of the data on which cause-of-death projections are based.


Add new comment