The product integral in practice

In a (much) earlier blog, Angus introduced the product-integral representation of the survival function:

\[{}_tp_x = \prod_0^t(1-\mu_{x+s}ds),\qquad(1)\]

where \({}_tp_x\) is the survival probability from age \(x\) to age \(x+t\) and \(\mu_{x+s}\) is the mortality hazard at age \(x+s\).  Regular readers of this blog (both of you) will notice a striking similarity with the Kaplan-Meier estimate of the survival function:

\[{}_t\hat p_x = \prod_{t_i\le t} \left(1-\frac{d_{x+t_i}}{l_{x+t^-_i}}\right),\qquad (2)\]

where \(\{x+t_i\}\) is the set of unique ages at death, \(d_{x+t_i}\) is the number of deaths at age \(x+t_i\) and \(l_{x+t^-_i}\) is the number of lives alive immediately before age \(x+t_i\).  The Kaplan-Meier estimate in equation (2) is the discretised equivalent of equation (1), meaning that \(d_{x+t_i}/l_{x+t^-_i}\) is an estimate of \(\mu_{x+t_i}(t_{i+1}-t_i)\).  Many actuarial portfolios quickly reach a size where there are events every single day of the year, making \((t_{i+1}-t_i)\) as small as \(\frac{1}{365}\).  This results in fairly smooth-looking Kaplan-Meier estimates, such as in Figure 1 below:

Figure 1.  Kaplan-Meier estimates of survival function from age 60 for a medium-sized Canadian pension plan, 2013-2019.

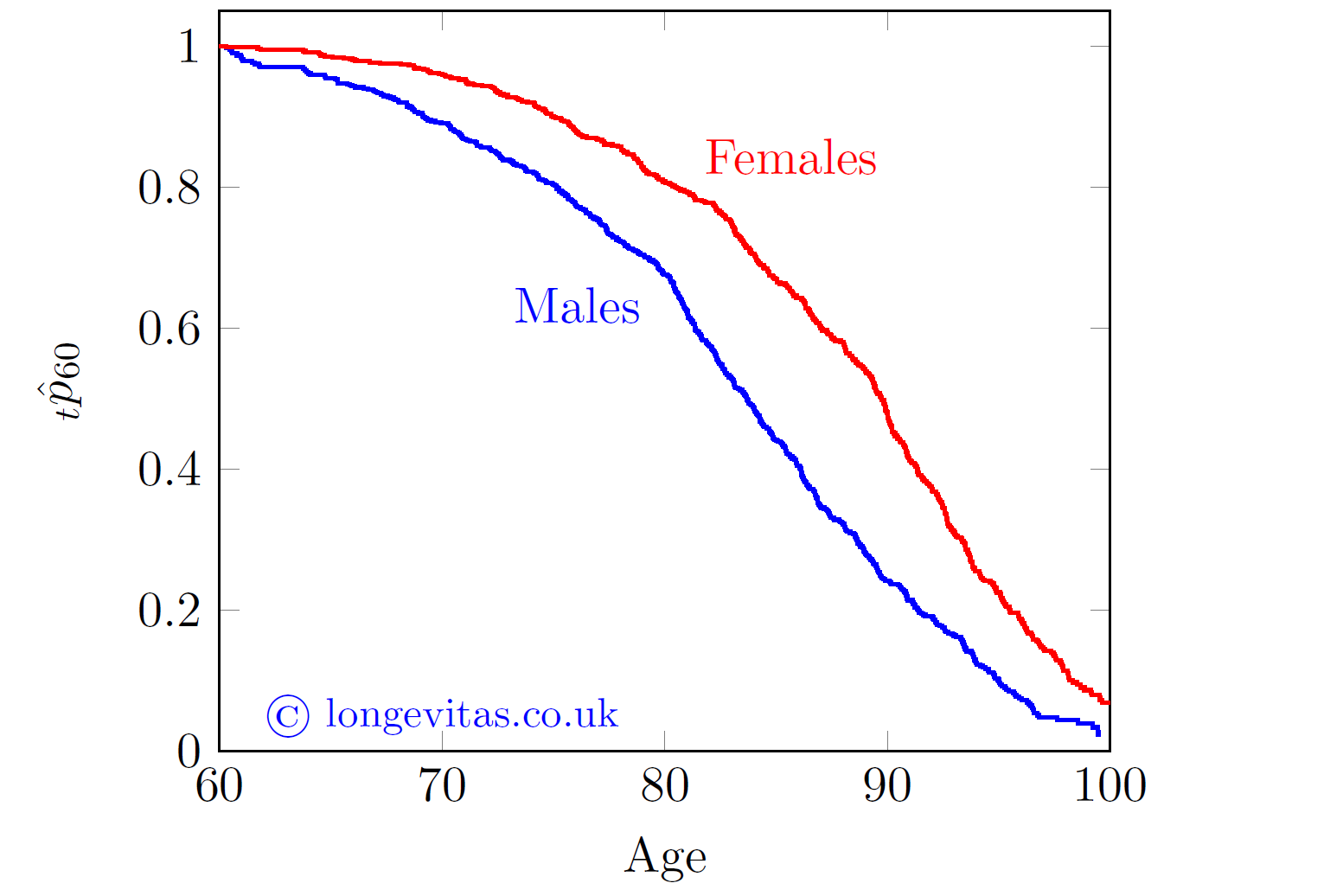
Behind Figure 1 lie 542 deaths among 3,871 females and 633 deaths among 3,141 males.  Despite the relatively modest amount of data, the Kaplan-Meier estimate is surprisingly smooth.

The Kaplan-Meier estimate is one of the first things I calculate in any mortality analysis - not only is it an excellent visual communication tool for non-specialists, it is also very useful for diagnosing data-quality problems before fitting any models.  Further examples of this are given in Richards and Macdonald (2024).