Volatility v. Trend Risk
The year 1992 was important in the development of forecasting methods: Ronald Lee and Lawrence Carter published their highly influential paper on forecasting US mortality. The problem is difficult: given matrices of deaths and exposures (rows indexed by age and columns by year) can we forecast future death rates? Lee and Carter designed a model specifically to solve this problem:
log μx,y = αx + βxκy (1)
where αx measures the average mortality at age x, κy measures the effect of year y; this year effect is modulated by an age dependent coefficient, βx. Lee and Carter used US data up to 1989 and here I’ve followed them by using data on US males aged 60–90 between 1933–1989, downloaded from the Human Mortality Database.
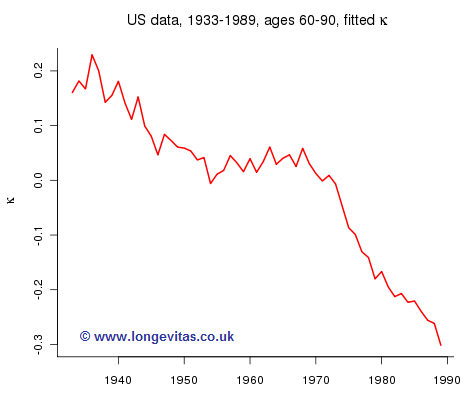
Now we see what they were up to. If we assume that the αx and βx are stable in time then all we need to do is forecast the κy in Figure 1. The model has reduced forecasting a table to forecasting a one-dimensional time series. Clever!
Now comes the tricky bit. What time series do we choose? Lee and Carter argued strongly from a plot similar to Figure 1 that the forecast should be based on a random walk with drift. Thus:
κy = κy-1 + a + εy, εy ˜ N(0, σ2), y = 1934, ... , 1989 (2)
where the drift and volatility parameters a and σ are to be estimated from the values of κy in Figure 1. We write this expression in terms of dy = κy - κy-1:
dy = a + εy, εy ˜ N(0, σ2), y = 1934, ... , 1989.
Our estimate of the drift parameter a is thus the mean of dy, about −0.008 for these data; the estimate of σ2 is the sample variance of dy, which gives a standard error of about 0.003 for our drift parameter. A very rough 95% confidence interval for a is (−0.014, −0.002) so a is not precisely determined. This has alarming consequences for the accuracy of our forecast. Figure 2 shows the best-estimate forecast for κ together with a 95% confidence interval:
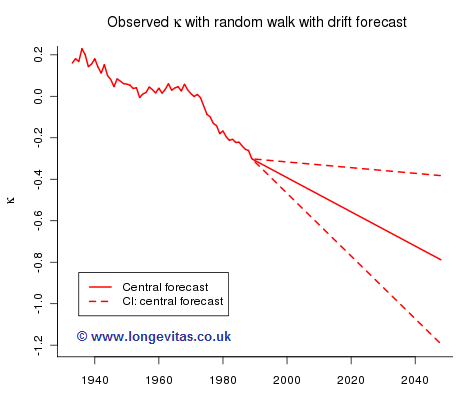
Future sample paths generated by model (2) depend on both parameter risk and stochastic risk. We can isolate stochastic risk and Figure 3 shows one hundred sample paths simulated under the assumption that the long term trend is fixed at the central forecast. The dashed green line is the 95% envelope, i.e. the probability that the envelope contains a sample path is approximately 0.95.
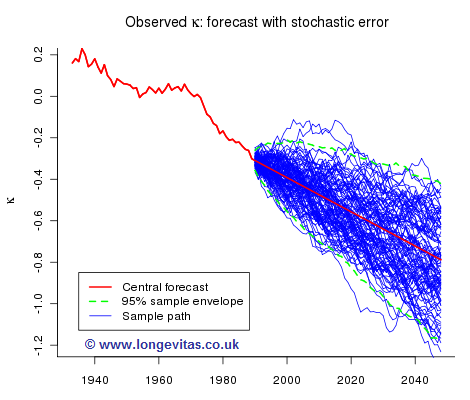
Figure 4 shows one hundred sample paths when only parameter uncertainty in the drift parameter is taken into account:
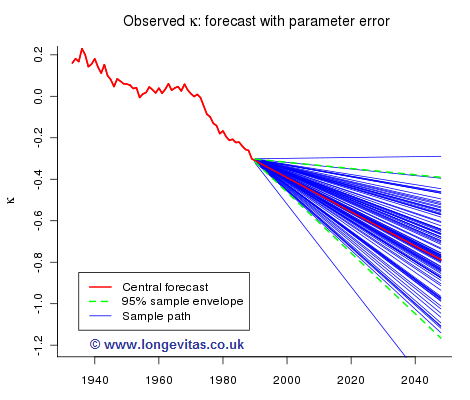
while Figure 5 shows one hundred sample paths when we allow for both parameter and stochastic risk:
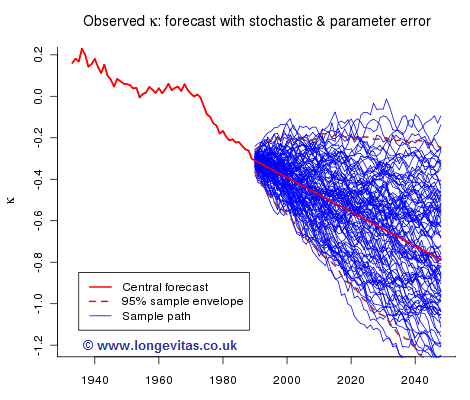
Figure 6 summarizes the relative contributions of parameter and stochastic risk:
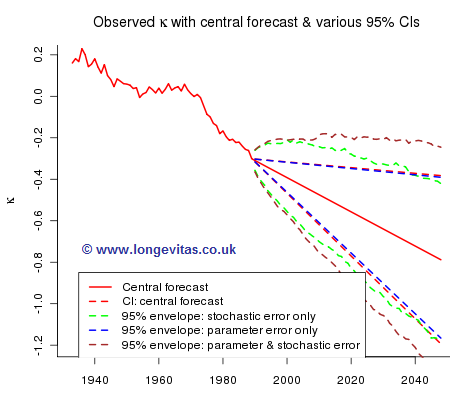
Here are a few of the many comments that can be made on this exercise:
- Volatility is the dominant source of error in the short term.
- The importance of long term trend gradually increases over time until it eventually overtakes volatility as the “senior partner”.
- The mean-reversion property of the random walk with drift is obvious in Figure 3. Are you comfortable that the course of future mortality behaves in this way? I merely ask the question.
And a final question: is there an elephant in the room? The above discussion assumes that the model is correct; there is no way we can be sure of this. A cautious actuary will consider a range of models. Only in this way can he or she come to an appreciation and understanding of longevity risk.
You can find some additional material in support of this blog in the technical note referenced below.
References:
Lee, R. D. & Carter, L. R. (1992) Modeling and forecasting US mortality. Journal of the American Statistical Association, vol 87, 659–675.
Currie, I. D. A technical note on estimating and forecasting with the random walk with drift.


Add new comment