A basis point

In an earlier post I mentioned the advent of survivor forwards, or S-forwards, a derivative contract which could be used for hedging pension liabilities.  Survivor forwards appeared again in another post illustrating the financial impact of model risk.

A survivor forward defined on an index of, say, population mortality will give a large data set with considerable history on which to base a projection model.  However, a natural question is to ask how suitable such a contract would be for hedging pension or annuitant liabilities?  Figure 1 shows the Kaplan-Meier survival curve from age 70 for male annuitants born in 1928, together with the corresponding survival curve for males in England & Wales.

Figure 1. Survival curves for male annuitants (red line) and males in England & Wales (black line). Source: Own calculations using ONS data for males in England and Wales, 1998–2006, and life-office annuitants over the same date range.

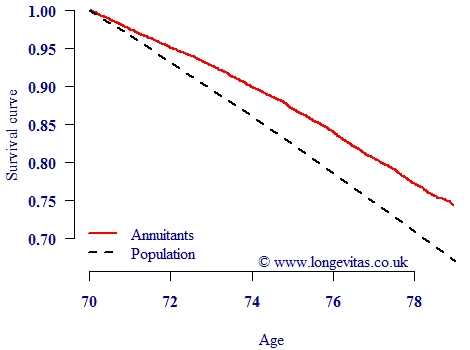
Figure 1 shows that life-office annuitants have a markedly higher survival rate than the population at large. This is unsurprising: people who have private pensions form a wealthier (and healthier) select sub-group of the wider population. However, one consequence of this is that a survivor forward defined on population mortality will in general be an imperfect hedge for most annuity portfolios or pension schemes. This is known as basis risk, and is well-known in other industries.  For example, airlines cannot hedge their jet-fuel costs directly, and so use imperfect hedges based on crude-oil or heating-oil futures.

As it happens, there are solutions to the divergence shown in Figure 1.  One solution is for the pension scheme to buy varying proportions of the underlying S-forwards to replicate the anticipated higher survival curve of holders of private pensions.  Another solution was discussed by Iain Currie in his post on modifying projections for basis risk.