Allowing for reporting delays

In a previous blog I outlined my six-month rule of thumb for discarding mortality experience affected by reporting delays. However, this can be awkward where there is a hard limit on how far back the experience data goes. For example, when a pension scheme switches administrator, or an insurer migrates business from one system to another, past mortality data is usually the first casualty. For example, I vividly remember starting a new job as head of mortality, only to discover that there was only 18 months of experience data available — a new annuity administration had gone into production, and nobody had thought to keep the experience data from the old system. I wish I could say that this situation was unique, but seventeen years of consulting tell me that it is not.

So what can an actuary do when discarding OBNR-affected data is an unaffordable luxury? Angus outlined one solution with a multi-state model. However, such models require secondary information on reporting delays, which is seldom available (so seldom in fact that I've never it seen in those seventeen years of consulting). An alternative approach is to define the OBNR-affected mortality hazard, \(\mu^{OBNR}_{x,y}\), as follows:

\[\mu^{OBNR}_{x,y} = \mu^*_{x,y}\rho(u_1-y,\lambda_1)\qquad (1)\]

where \(\mu^*_{x,y}\) is the underlying mortality at age \(x\) at time \(y\) that we are really interested in. \(u_1\) is the time of the data extract, say the day after the last date of death in the experience data. \(\rho(s,\lambda_1)\) is the allowance for the OBNR effect — \(s>0\) is the time until the extract date, and \(\lambda_1\) is a decay parameter that controls how quickly the OBNR effect falls from 1 to zero. Some example OBNR functions are given below and plotted in Figure 1:

\begin{eqnarray*}{\rm Logistic} &:& se^{\lambda_1}\\{\rm Exponential} &:& 1-\exp\left(-se^{\lambda_1}\right)\\{\rm Inverse\ tangent} &:& \frac{2}{\pi}\tan^{-1}(se^{\lambda_1})\\{\rm Gaussian} &:& 2\Phi\left(se^{\lambda_1}\right)-1\\{\rm Inverse\ exponential} &:& 2\left(1+\exp\left(-se^{\lambda_1}\right)\right)^{-1}-1\\{\rm Squared\ exponential} &:& 1-\exp\left(-s^2e^{\lambda_1}\right)\end{eqnarray*}

Figure 1. OBNR functions with \(\lambda_1=2\). Source: Richards (2021). Note that the horizontal axis is reversed.

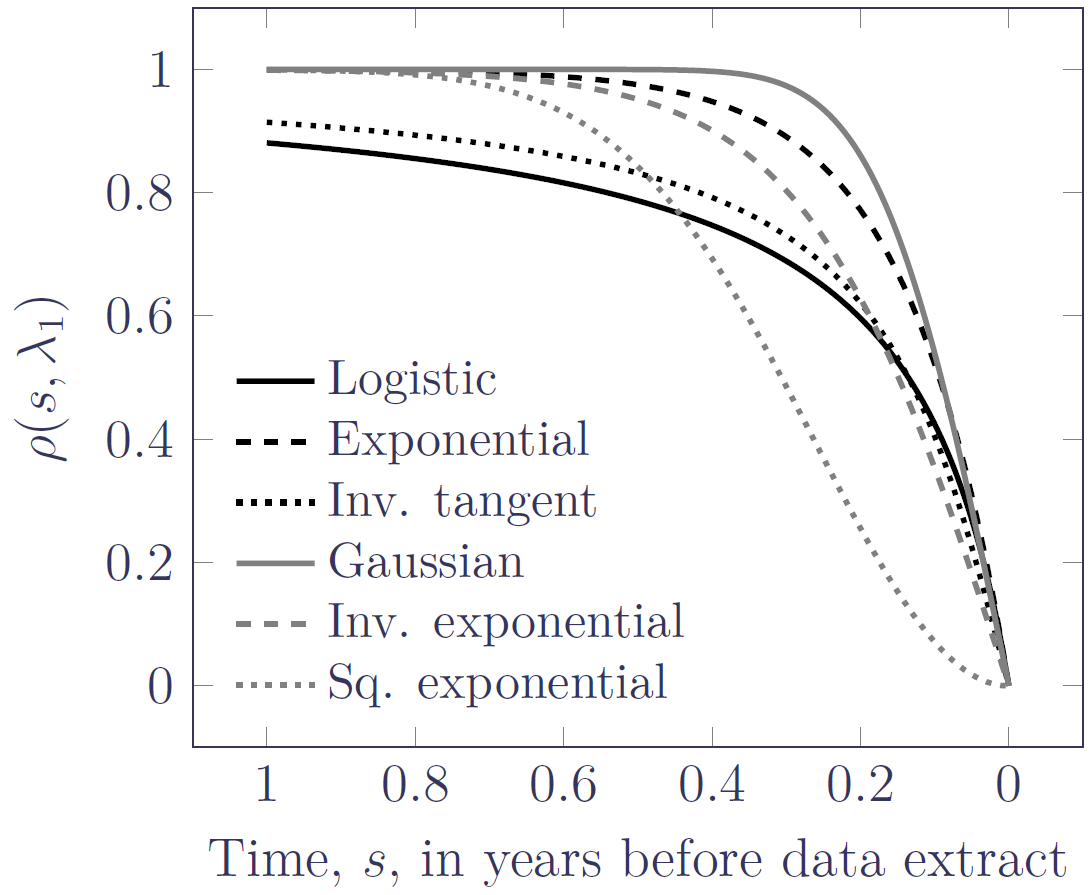
Figure 1 shows that the OBNR functions vary in the degree to which they decay from close to 1 down to zero. We can therefore fit our mortality models using \(\mu^{OBNR}_{x,y}\) to allow for the OBNR effect; \(\lambda_1\) will be estimated along with the other parameters. In the same way that we select risk factors using an information criterion like the AIC, we can try the various OBNR functions above to see which one of them fits best.

The left panel of Figure 2 shows the monthly deviance residuals in a model for the mortality of annuitants in France. The large negative residuals on the right are the consequence of unreported deaths in the months leading up to the extract date. The right panel of Figure 2 shows the monthly deviance residuals for the same model including a Gaussian OBNR term (with \(\lambda_1=1.32332\)). The disappearance of the large negative residuals shows that the impact of OBNR has been removed, meaning that the rest of the model's parameters are no longer affected and all the experience data can be used to calibrate the model.

Figure 2. Monthly deviance residuals for model without OBNR allowance (left panel) and with OBNR allowance (right panel). Source: Richards (2021).

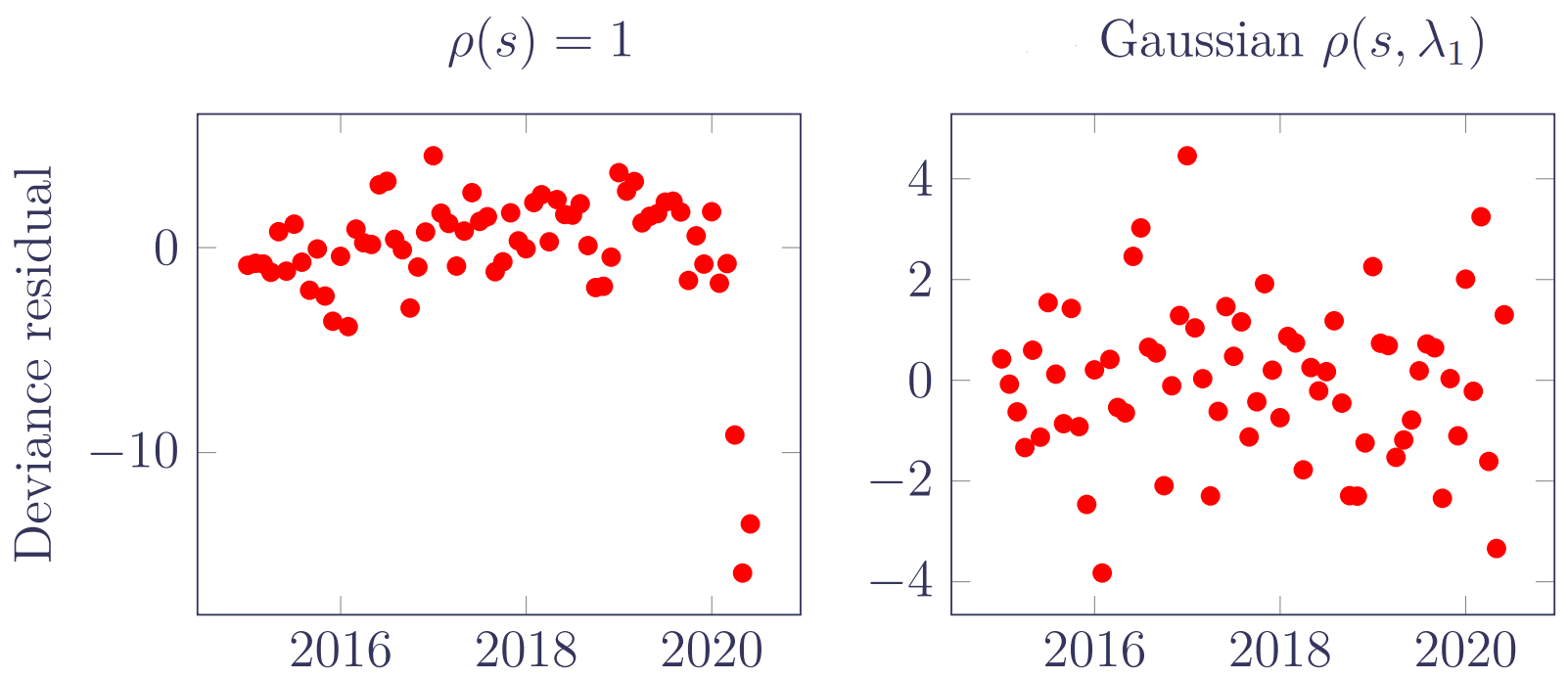
The interesting aspect of Figure 2 is that OBNR has been allowed for with a single data extract and without any secondary data on the history of reporting delays. We note in passing that the model for \(\mu^*_{x,y}\) should contain both a time trend and a seasonal effect to avoid confounding with the OBNR effect. Nevertheless, adding an OBNR term to a model allows the analyst to make the most of all available experience data.