Features of the survival curve
The survival curve is simply the proportion of lives surviving to each age. Below is an example for males at initial age 60 in the United Kingdom, using the Interim Life Table from the Government Actuary's Department:
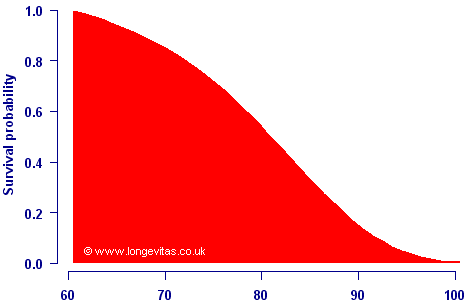
The survival curve starts at 1 (or 100%) as everyone is alive at outset, and decreases monotonically towards zero (or 0%) as people die. The survival curve is better known to actuaries as tpx, the probability of a life aged x surviving to age x+t. An oft-unappreciated feature of the survival curve is that the area underneath it is simply the life expectancy.
Instead of plotting the survival curve, exactly the same data can be used plot the distribution of age at death:
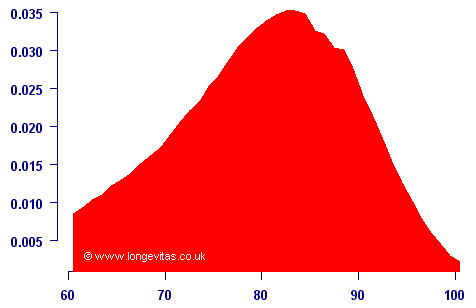
The graph above is known to actuaries as the curve of deaths, and was long ago recognised as often being easier to deal with than mortality rates.
Another way of looking at the curve above is that it is the probability density function for the age at death. A survival model implicitly assumes that the future lifetime is a random variable, Tx. The probability density function for Tx is simply tpxμx, which is the curve of deaths plotted above. Thus, a survival model is the same as assuming that future lifetime is a random variable. The converse is also true: assuming a probability distribution for the future lifetime is a survival model.


Add new comment