Hitting the target, but missing the point
Targeting methods are popular in some areas for mortality forecasting. One well known current example is the CMI's model for forecasting mortality. The CMI model allows the user to fix the long-term mortality-improvement rate; Stephen has written previously about some of the undesirable consequences of this, while Gavin has written about dealing with its lack of an uncertainty measure. However, other consequences of a targeting assumption are less well known, so we will explore them here. We present a simple example which illustrates the impact that an assumption about the future — which after all is what a target is — can have on a forecast.
To illustrate, we use male mortality data, i.e. death counts and central exposures, for age 65 from 1961 to 2009 from the ONS data set for England and Wales. Suppose we wish to forecast mortality to 2051. There are many ways of approaching this problem but we will use the method of P-splines; see Richards, Kirkby and Currie (2006) for a description of the method from an actuarial perspective. Figure 1 shows the data together with the resulting central forecast and its 95% confidence interval. The central forecast looks plausible and the expanding funnel of doubt reflects our increasing uncertainty about the course of mortality as we look further into the future.
Figure 1. Observed and projected mortality rates at age 65 (logarithmic scale), together with confidence envelope. Source: own calculations using ONS data for males in England & Wales.
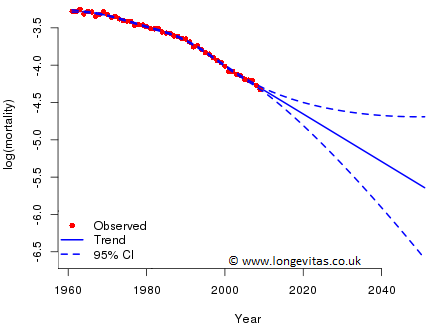
The central forecast for the log(mortality rate) in 2051 is -5.642, so the central mortality rate at that time is 0.00355 (=exp(-5.642)). Suppose we now target this value of mortality, i.e. we assume that the value -5.642 is known. To do this we will specify a target rate indirectly by providing dummy counts for deaths and exposures. We do this as follows: the number of male births in 1986 was 335,478; from ELT 16 we find that l65/l0 = 0.83328, so an estimate of the exposure at age 65 in 2051 is 280,000 approximately. Hence, the "number" of deaths is 933, since the force of mortality is 0.00355 by assumption. We then add these pseudo-data points for deaths and exposures to our data set and refit. Figure 2 shows the result.
Figure 2. Observed and projected mortality rates at age 65 (logarithmic scale), using a target value for 2051. Source: own calculations using ONS data for males in England & Wales.
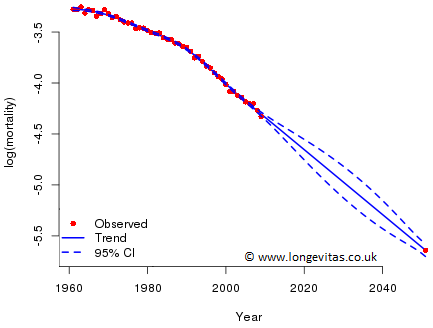
The central forecast is unchanged but the 95% confidence interval is very different. Initially we see an expanding funnel of doubt but even in the early years of the forecast the influence of the target is evident; the confidence interval is much narrower. Around halfway through the forecast period the confidence interval actually starts to narrow until at the target our forecast is made almost without error.
It seems axiomatic that our knowledge of the future should become less certain as we look further ahead; the expanding funnel of doubt in Figure 1 is simply an expression of this "axiom". Any forecasting method which violates this should therefore be viewed with suspicion. One could even go further: any forecasting method should pass the expanding-funnel-of-doubt test, i.e. it must produce confidence intervals that widen with time. This test raises some awkward questions for both deterministic and targeting methods of forecasting.
References:
Richards, S. J., Kirkby, J. G. and Currie, I. D. (2006) The importance of year of birth in two-dimensional mortality data (with discussion), British Actuarial Journal, 12, 5–61.


Add new comment