Are annuities expensive enough?

The rationale of any business is to make a profit.  This is usually achieved by selling things for more than they cost to make or supply.  The annuities business is no different: an insurer in the UK will typically charge around 5% more than it expects the annuity to cost.  The twist is that it takes many years to find out how much profit is actually made (or if any profit was made at all).

Of course, mortality is a random process as no-one can say for sure when an annuitant will die.  This means that the profit on an annuity is also a random variable.  Figure 1 shows the probability distribution of the profit on a level annuity payable annually in advance to a male aged 60.

Figure 1. Probability distribution of discounted profit relative to initial expected cost for a level annuity payable in advance to a male aged 60. Mortality according to PCA00 without future improvements, cashflows discounted at 3% per annum.

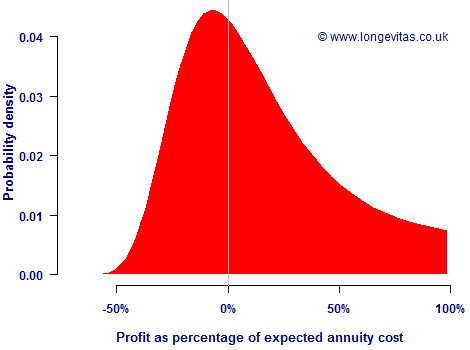
Figure 1 shows an interesting feature about the profitability of annuities, namely the profit distribution is rather lop-sided.  This has some consequences worth noting:

1. The modal outcome (peak of probability distribution) is on the negative side.  While the insurer will make a profit of 5% on average, the likeliest single outcome for one annuity (rounded to the nearest percentage) is actually a loss of -12% in this example.  To place the mode on the break-even point of zero would require a profit margin of around 12% here instead of 5%.
2. Expected profitability is heavily dependent on the rates of mortality in the first few years after the contract is written: mortality in the early years generates the large positive profit percentages on the right.  In this example the entire profit margin is supplied within the first seven years.
3. If the actual rates of mortality are lower than expected in the first few years, this has a disproportionately large impact.  Correct estimation of the initial rates of mortality for an annuitant is therefore critical for profitability.

The dependence on profitability on the first few years of mortality is lent extra piquancy because writing annuities is a leveraged business.  One of the best ways an insurer can guard its profitability is to correctly estimate rates of mortality in the first years of an annuity.  In an earlier post we saw that survival models use more information on the first few years after retirement, and are therefore preferable to models based on q_x rates.