The interrupted observation

A common approach to teaching students about mortality is to view survival as a Bernoulli trial over one year. This view proposes that, if a life alive now is aged \(x\), whether the life dies in the coming year is a Bernoulli trial with the probability of death equal to \(q_x\).  With enough observations, one can estimate \(\hat q_x\), which is the basis of the life tables historically used by actuaries.

However, viewing mortality as a series of annual Bernoulli trials often doesn't correspond to reality.  In particular, the Bernoulli view of mortality only permits two outcomes:

1. The life is observed to have died during the year, or

2. The life is observed to have survived the year.

By definition, the Bernoulli trial doesn't permit a third option, namely that the life ceases observation during the year, meaning that one doesn't know if the life has died or not.  This is illustrated in Figure 1, where around 60,000 annuities in a portfolio ceased observation in 2013 because they were transferred to another insurer:

Figure 1.  Number of in-force annuities for UK insurer.  Source: Richards & Macdonald (2024, Figure 3a).

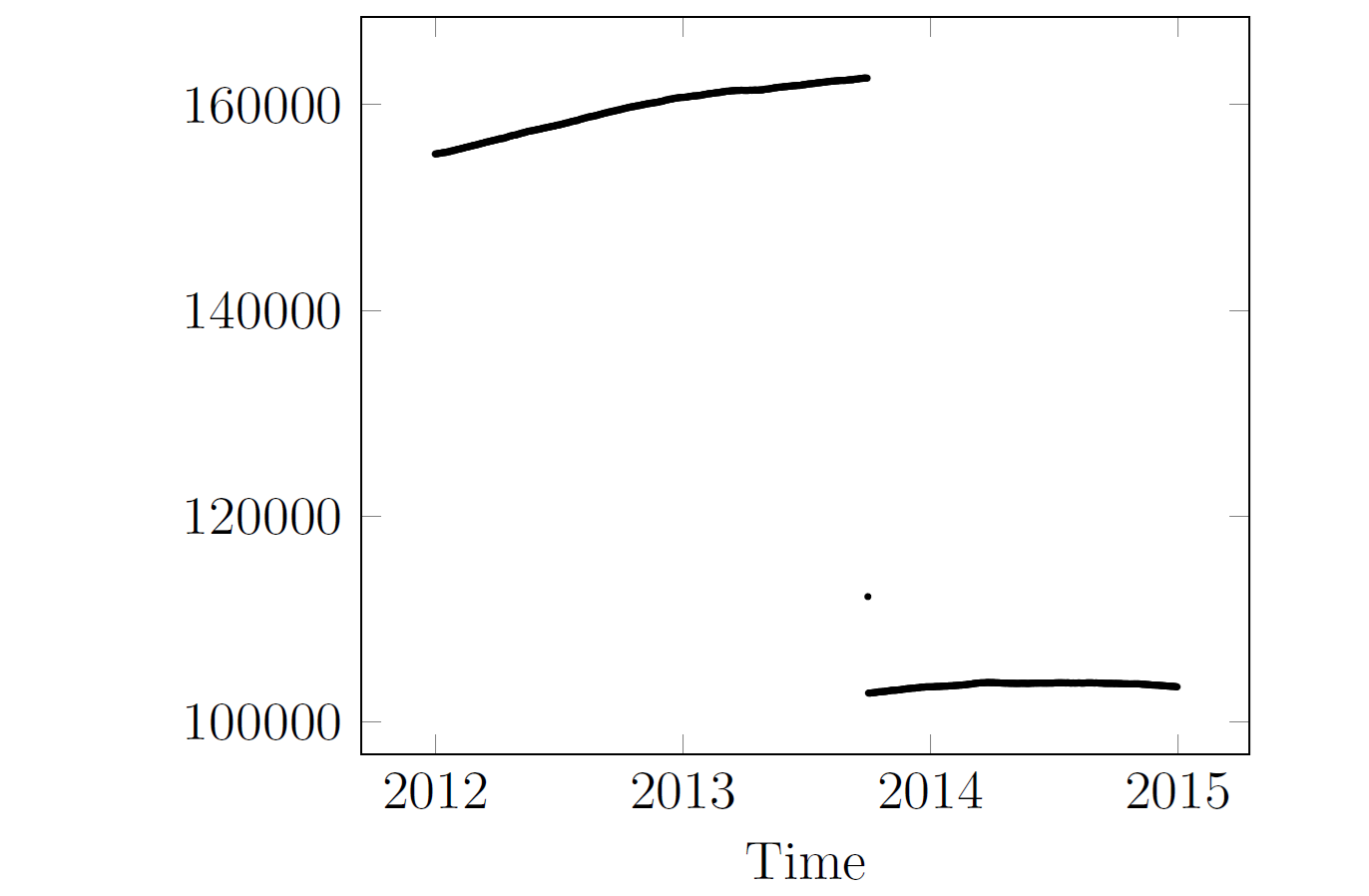
There are many reasons why observation of in-force annuities and pensions might cease during a year: change of pension administrator, selective buy-out of pension liabilities or commutation of small pensions.  It is clear that the idea of mortality as a Bernoulli trial over a year is a simplification used as a teaching aide.  Pratchett et al (1999) described such simplifications as 'lies-to-children':

The early stages of education have to include a lot of lies-to-children, because early explanations have to be simple.  However, we live in a complex world, and lies-to-children must eventually be replaced by more complex stories

Pratchett et al (1999, page 43)

So what would be the more complex replacement story for mortality?  One obvious answer is a model that copes with interrupted observations of the sort in Figure 1.  This can be achieved with a survival model.  Instead of fixing a arbitrary period and observing whether a life dies or not, we instead observe an information pair \((t_i, d_i)\):

• \(t_i\) is the time observed for life \(i\), and

• \(d_i=1\) if the life died at time \(t_i\) (and \(d_i=0\) otherwise).

This alternative set-up is illustrated in Figure 2:

Figure 2.  Observation of individual lives A, B and C in a survival model.  Source: adapted from Richards and Macdonald (2024, Figure 1).

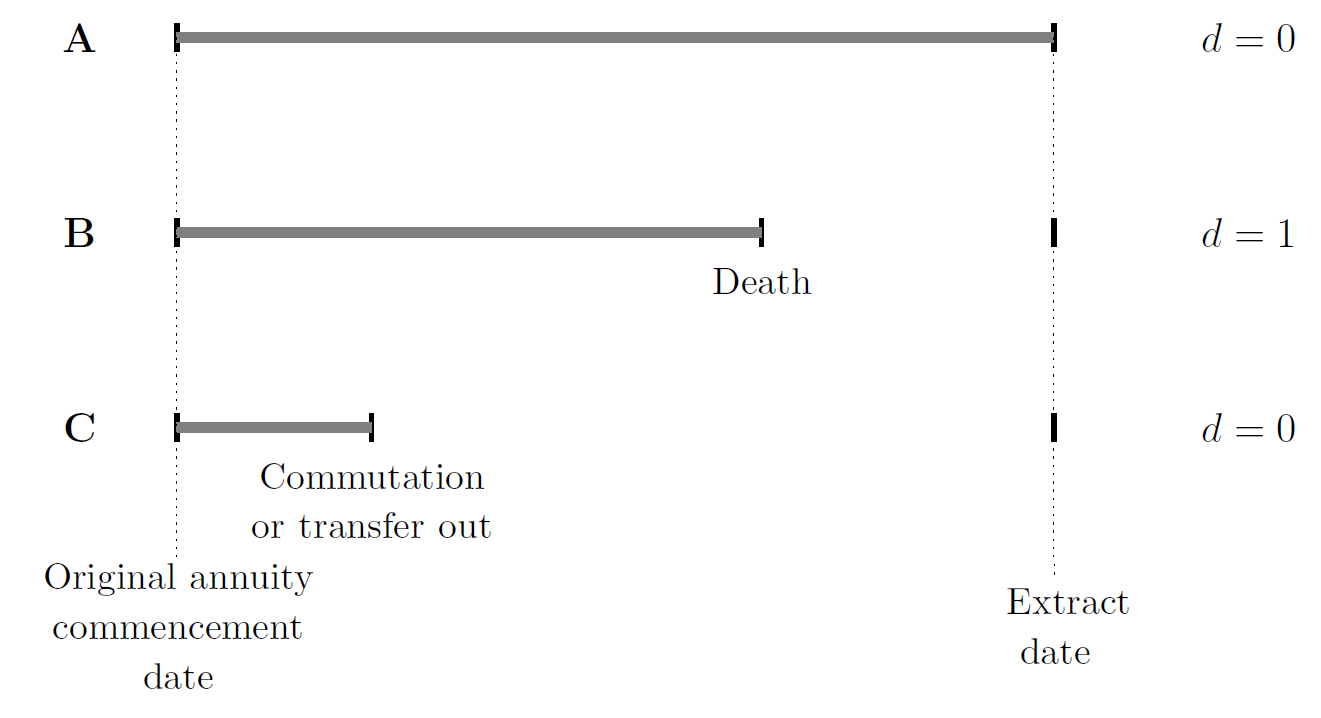
In Figure 2 we have observation of lives from pension commencement to the date an extract is taken for experience analysis.  Analogous to the Bernoulli view, Case A covers survival to the end of the period and Case B covers death during the period.  However, Case C additionally shows how a survival model copes with exits from observation - the life was under observation for a period of time and could have died, but observation ceased before the extract date.  Mathematically, both A and C are right-censored, i.e. we do not know when or if they have died; all we know is that they were alive at times \(t_A\) and \(t_C\) when they were last observed.  The view of mortality as a pairing of the survival time (\(t\)) and the indicator variable (\(d\)) is the more complex story that allows us to model the reality of real-world business processes.