Real-time decision making

In a previous blog I looked at how continuous-time methods can provide real-time management information.  In that example we tracked the (almost daily) development of the mortality of two tranches of new annuities, as shown again in Figure 1.

Figure 1.  Cumulative hazard, \(\hat\Lambda(t)\), for new annuities written by French insurer.  Source: Richards and Macdonald (2024).

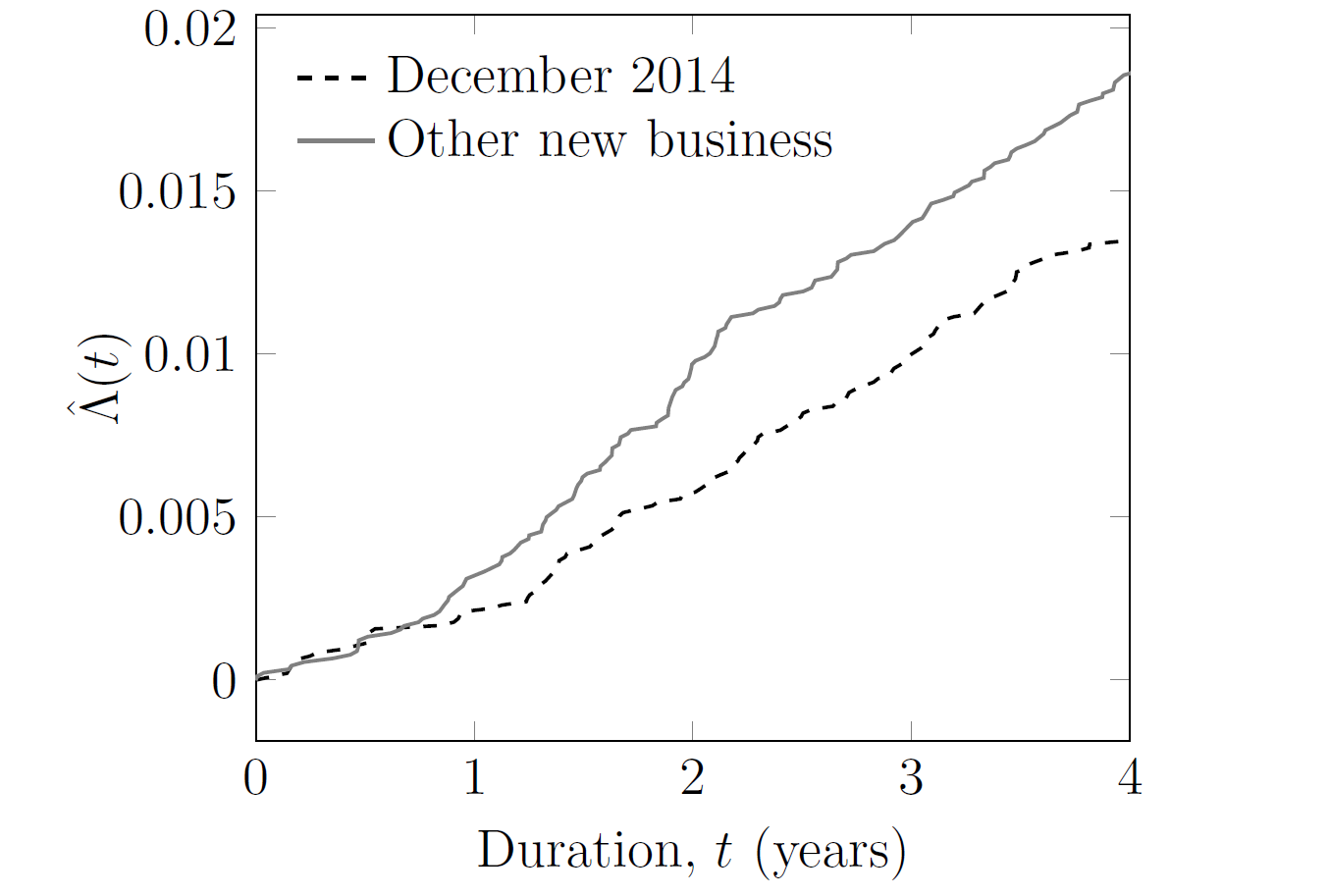
Figure 1 uses \(\hat\Lambda(t)\), the Nelson-Aalen estimator of the cumulative risk or cumulative hazard:

\[\hat\Lambda(t)=\sum_{t_i\leq t}\frac{d_{t_i}}{l_{t_i^-}},\qquad(1)\]

where \(\{t_i\}\) is the set of distinct durations at death since annuity outset, \(l_{t_i^-}\) is the number of annuities in-force at duration \(t_i\) and \(d_{t_i}\) is the number of those annuities ceasing due to death at that duration.  The December 2014 tranche of new annuities has materially lower mortality, and the use of continuous-time methods allows the analyst to detect this sooner than using annual \(q_x\)-style mortality rates.  But how much sooner?  And with what degree of certainty?

To answer this we want to place a confidence funnel on one of the cumulative hazards in Figure 1 to see if the other cumulative hazard lies outwith it.  We start with an estimator for the mean squared error, \(\hat\sigma^2(t)\), of the Nelson-Aalen estimator, \(\hat\Lambda(t)\).  From Andersen et al (1993, equation 4.1.6) we have:

\[\hat\sigma^2(t) = \sum_{t_i\leq t} \frac{d_{t_i}}{(l_{t_i^-})^2}.\qquad(2)\]

The next step is to use the mean squared error to form a confidence envelope.  There are several options, each with different properties; see Section IV.1.3 of Andersen et al (1993).  The one we use here is from Bie et al (1987), which is a symmetric confidence interval on the logarithmic scale:

\[\log \hat\Lambda(t)\pm c_{\alpha/2}\frac{\hat\sigma(t)}{\hat\Lambda(t)},\qquad(3)\]

where \(c_{\alpha/2}\) is the upper \(\alpha/2\) fractile of the standard normal distribution, e.g. 1.96 for a 95% confidence envelope.  This gives rise to an asymmetric confidence envelope on the original scale:

\[\hat\Lambda(t)\exp\left(\pm c_{\alpha/2}\frac{\hat\sigma(t)}{\hat\Lambda(t)}\right).\qquad(4)\]

Figure 2 reprises Figure 1, but with the 95% confidence envelope in grey for the  non-December 2014 tranche of annuities.

Figure 2.  Cumulative hazard, \(\hat\Lambda(t)\), for new annuities written by French insurer, with 95% confidence envelope in grey for non-December 2014 tranche using the expression in (4).

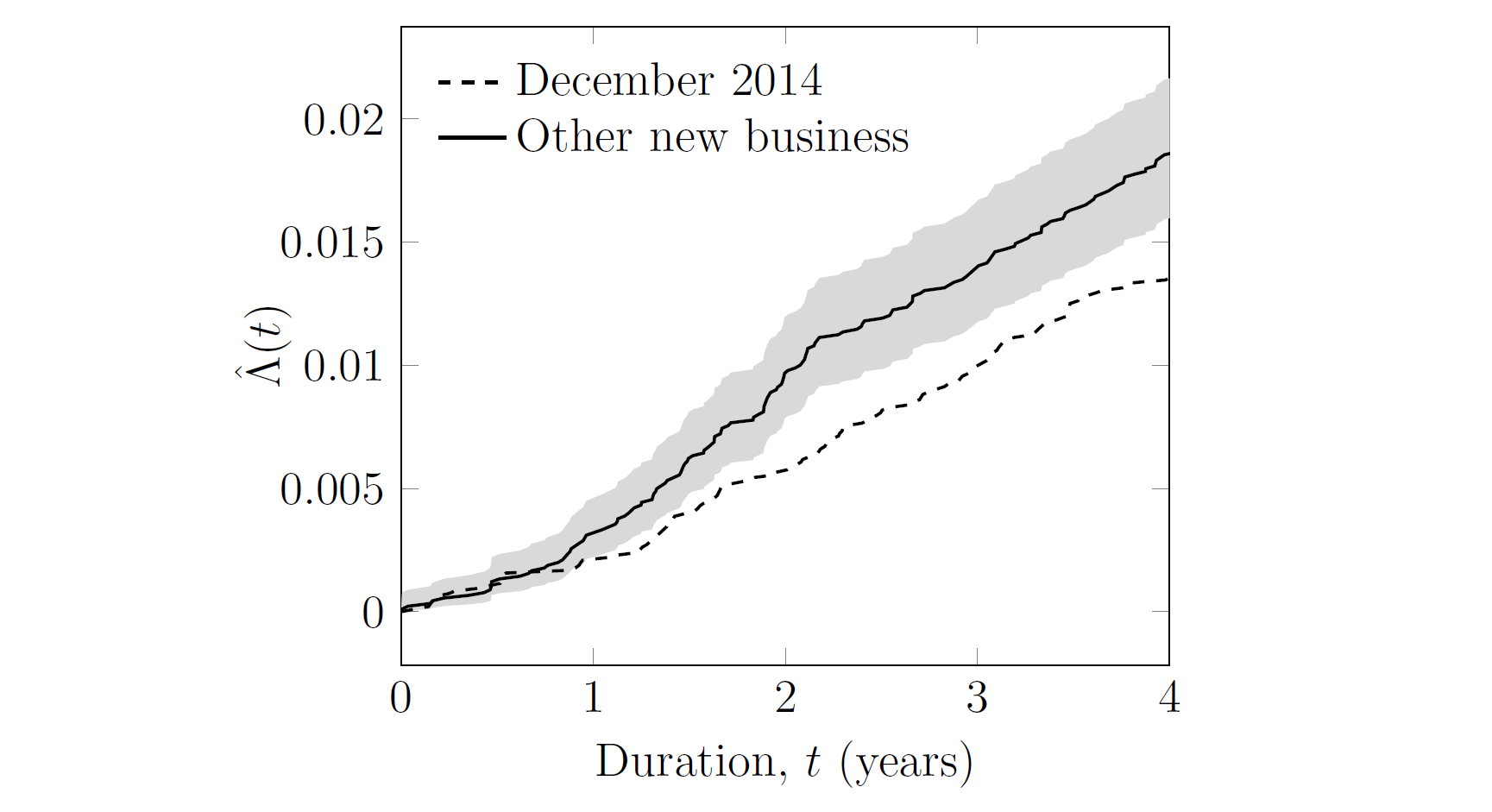
Figure 2 shows that continuous-time methods allow the detection of a difference in mortality shortly after the first anniversary of the December 2014 tranche, say in early 2016.  In contrast, Figure 1 shows that the user of annual \(q_x\) rates would have needed to wait a further year to reach this conclusion, i.e. early 2017.

Alternatively, we could place the confidence envelope around the December 2014 tranche of annuities, as in Figure 3.  However, the conclusion is the same: continuous-time methods give better advanced warning than annual \(q_x\) analysis.

Figure 3.  Cumulative hazard, \(\hat\Lambda(t)\), for new annuities written by French insurer, with 95% confidence envelope in grey for December 2014 tranche using the expression in (4).

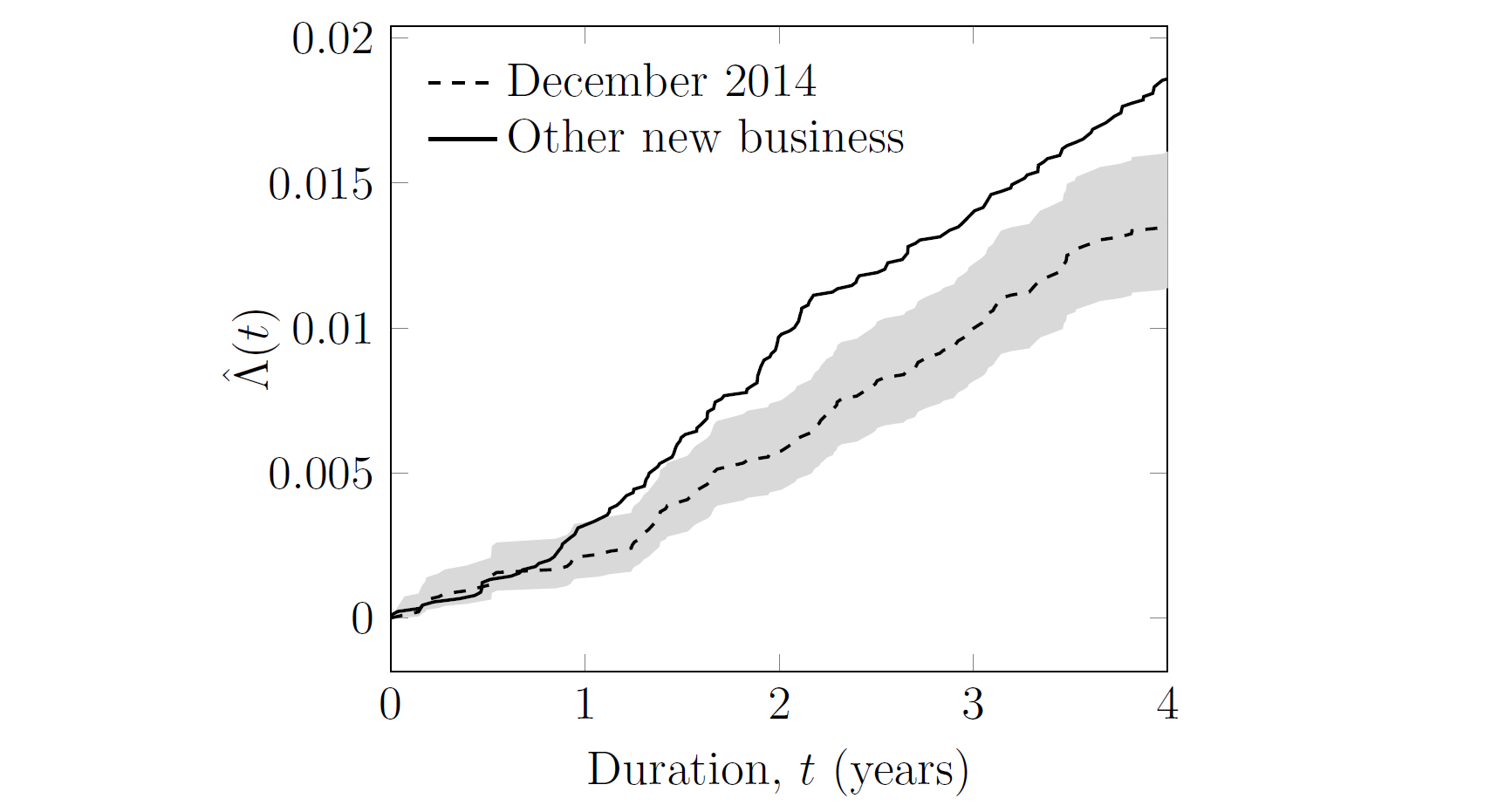
One thing insurers need to be wary of is duplicates, i.e. where an individual has more than one policy. If so, the confidence intervals in the likes of Figures 2 and 3 will be understated.  The preferred solution is of course to carry out deduplication, although this becomes tricky if the various annuities held by the same person have different start dates.