Robust mortality forecasting for univariate models
The covid-19 pandemic led to high levels of mortality in many countries in 2020. Figure 1 shows that the number of deaths in England & Wales in 2020 was an outlier compared to preceding years.
Figure 1. Total deaths by calendar year for females in England & Wales. Source: HMD data, ages 50–105.
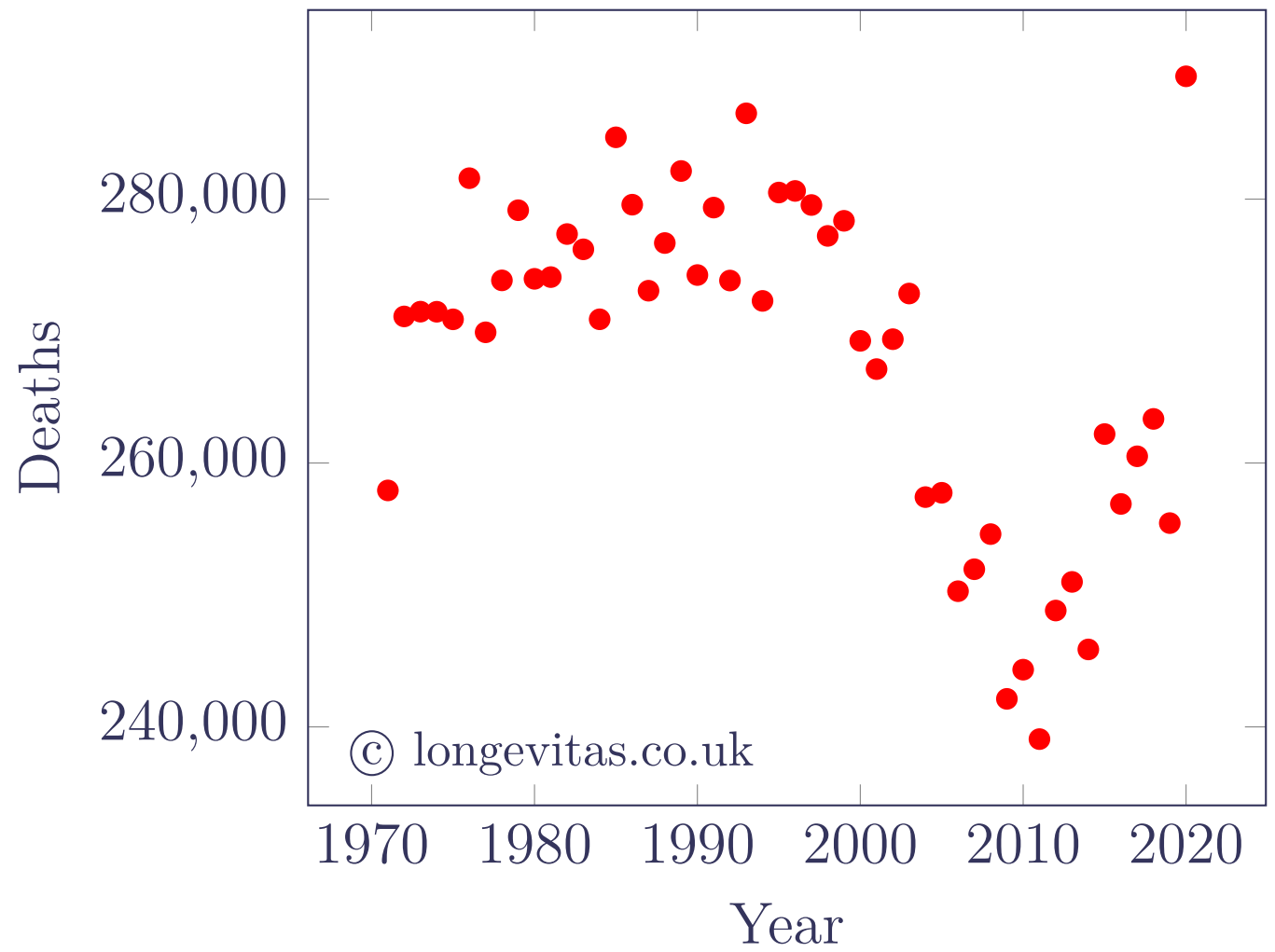
Outliers such as the 2020 experience are a problem for mortality forecasting models. Without adjustment, statistical models will have parameters biased by the 2020 data. For insurance work this means not only that forecasts are biased, but also that value-at-risk (VaR) capital requirements will be overstated. This is because outliers disproportionately inflate the error variance, and Kleinow & Richards (2016) showed that this is a major driver of VaR-style capital requirements.
The immediate response of most actuaries was to ignore the 2020 data and to continue using models calibrated up to 2019. This was a practical response to a highly unusual situation. However, ignoring the mortality experience of one or two years is not a permanent solution, and more rigorous approaches are required. Fortunately, statisticians in other fields have long worked on the handling of outliers, and there are well-researched methods of dealing with outliers that actuaries can apply.
It is well known that maximum-likelihood methods can be very sensitive to the presence of outliers in the data. As a result, much initial work on robustification focused on robustifying the likelihood through use of influence functions. An influence function is designed to behave much like the log-likelihood while an observation is a sensible distance from the mean, but to limit the contribution of extreme values. What counts as “extreme” varies by researcher, but many opted for a critical threshold of 3 standardised deviations — with a Normally distributed sample, only around 0.3% of observations should be that far away from the mean. Martin, Samarov & Vandaele (1982) examined in detail how to robustify the log-likelihood function for fitting an ARIMA model.
However, robustifying the log-likelihood has drawbacks. It is undesirable to use an influence function classified as a hard rejection function, since this leads to cliff-edge behaviour: why should an observation 2.99 standardised deviations from the mean contribute fully to the log-likelihood, while an observation that is 3.01 standardised deviations away is excluded entirely? The preference was therefore for a smoother progression in influence, but this in turn leads to reduced efficiency: observations around 1.5-2 standardised deviations away from the mean make less of a contribution to the log-likelihood than those closer to the mean, thus making less than full use of all available data.
Later work moved away from robustifying the log-likelihood towards identifying and quantifying the outlier effects. Such methods are fully efficient in that each observation contributes equally to parameter estimation, but the identification and quantification of outlier effects removes the undesirable bias in the rest of the model. A good example of this is the methodology of Chen & Liu (1993), which applies to univariate ARIMA models of the type used for APC and Lee-Carter models. An example of a Lee-Carter model robustified using Chen & Liu’s approach is shown in Figure 2.
Figure 2. Estimated and forecast values of log(mortality hazard) at age 75 for Lee-Carter model of mortality for females in England & Wales. Source: own calculations using the approach of Chen & Liu (1993) with a critical value of 3; HMD data for females, ages 50–105.
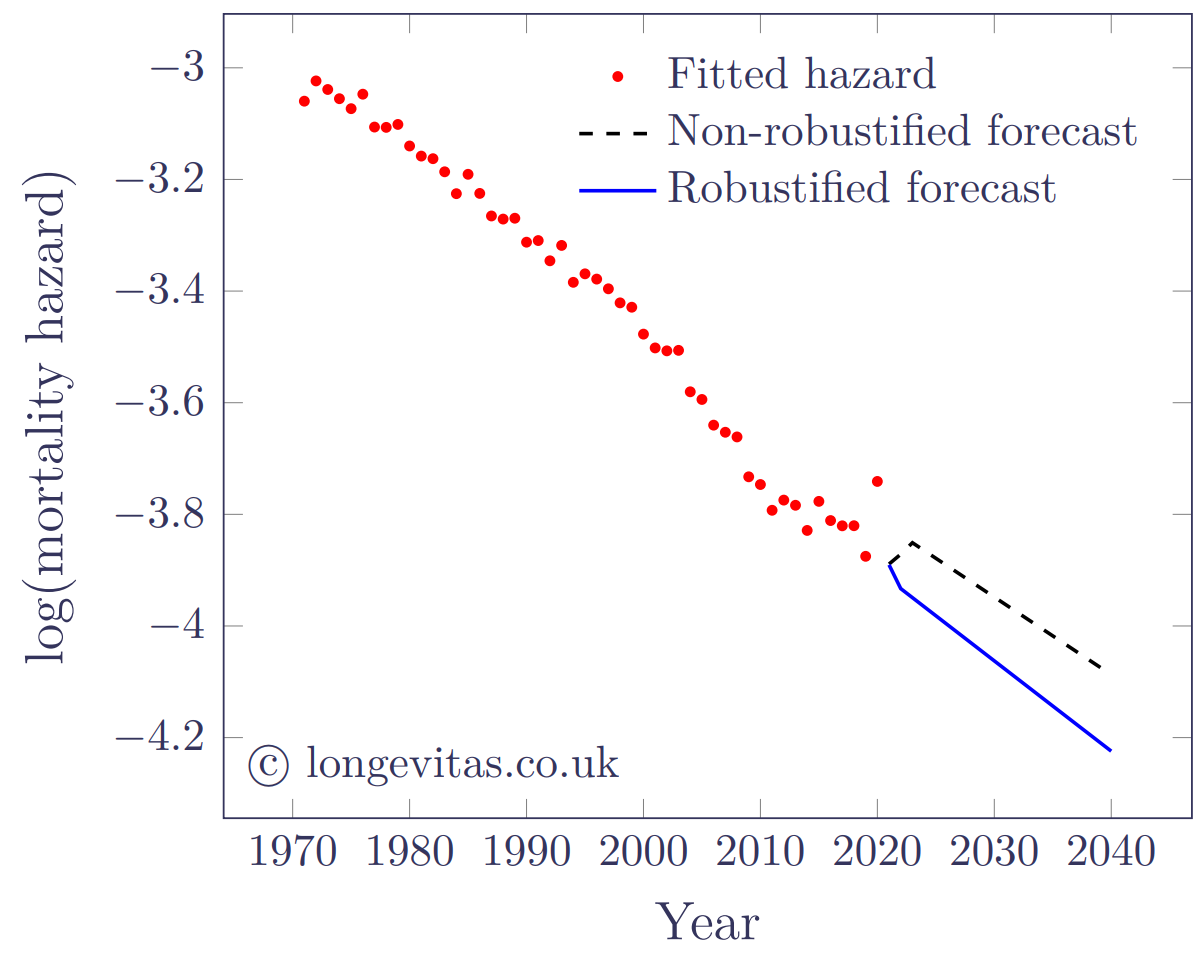
The Chen-Liu approach identifies an additive outlier in 2020, as expected: the estimated outlier effect is 0.059123 with a t-value of 4.95. In addition to removing bias from parameter estimates (see Table 1), the estimation of the outlier effect allows the forecast starting point can also be robustified by deducting the outlier effect from the observed value.
Table 1. ARIMA(0,1,3) parameter estimates for time index for Lee-Carter model of mortality for females in England & Wales. Source: own calculations using Chen-Liu robustification with a critical value of 3, HMD data for ages 50–105.
| Parameter | Non-robustified | Robustified |
|---|---|---|
| ma1 | -1.014 | -0.841 |
| ma2 | 0.522 | 0.306 |
| ma3 | 0.351 | 0.513 |
| Mean (μ) | -0.00737 | -0.00858 |
| Volatility (σ2) | 0.000193 | 0.000129 |
Table 1 shows how different parameter estimates are between robustified and non-robustified model fits.
References:
Chen, C. and Liu, L-M. (1993) Joint Estimation of Model Parameters and Outlier Effects in Time Series, Journal of the American Statistical Association, March 1993, Vol. 88, No. 421, pages 284–297.
Kleinow, T. and Richards, S. J. (2016) Parameter risk in time-series mortality forecasts, Scandinavian Actuarial Journal, 2016(10), pages 1–25.
Martin, R. D., Samarov, A. and Vandaele, W. (1982) Robust methods for ARIMA models, Department of Statistics, University of Washington, Seattle, March 1982, Technical Report No. 21.
Previous posts
Portfolio mortality tracking: USA v. UK
In Richards (2022) I proposed a simple real-time mortality tracker that can be implemented in a spreadsheet or R. The tracker is useful for exploratory analysis, spotting data-quality issues and communication with non-specialists. To recap, we require just three items of data:
Dr. Iain D. Currie
It is with great sadness that we note the passing of our long-term collaborator, Dr. Iain D. Currie, on 24th May 2022.


Add new comment