Seasonal patterns in mortality

During an analysis of a large annuity portfolio we took some time out to look at the pattern of mortality by season as well as the overall time trend. We fitted a model for age, gender and season, where the definition of season is that used by the ONS: each season covers three months, and where winter covers December, January and February. The results are shown below, where the mortality index has a value of 100 in January 1998.

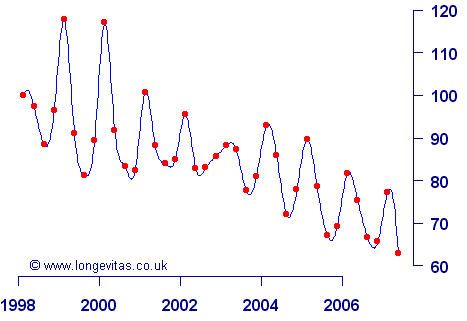
The chart shows a number of interesting features. Most obviously, there is a strong downward trend, reflecting the ongoing significant improvements in annuitant mortality in the United Kingdom.

The next feature is the strong cyclic intra-year patter: high mortality in winter months, followed by lighter mortality in summer months.

There is also evidence of negative autocorrelation: winters with very heavy mortality tend to be followed by summers with very light mortality. The years 1999 and 2000 show a very wide amplitude due to this.

One conclusion to draw from this is the importance of analysing mortality over as long a time period as possible to reduce the influence of period effects.