A spline primer

A spline is a mathematical function.  They are used wherever flexibility and smoothness are required, from computer-aided design and cartoon graphics, to the graduation of mortality tables (McCutcheon, 1974).  There are numerous different types of spline, but the most common is the spline proposed by Schoenberg (1964).  Figure 1 shows Schoenberg splines of degrees 0–3, all of which start in 2015:

Figure 1. Schoenberg (1964) splines of degree 0–3 with first non-zero value from 2015.

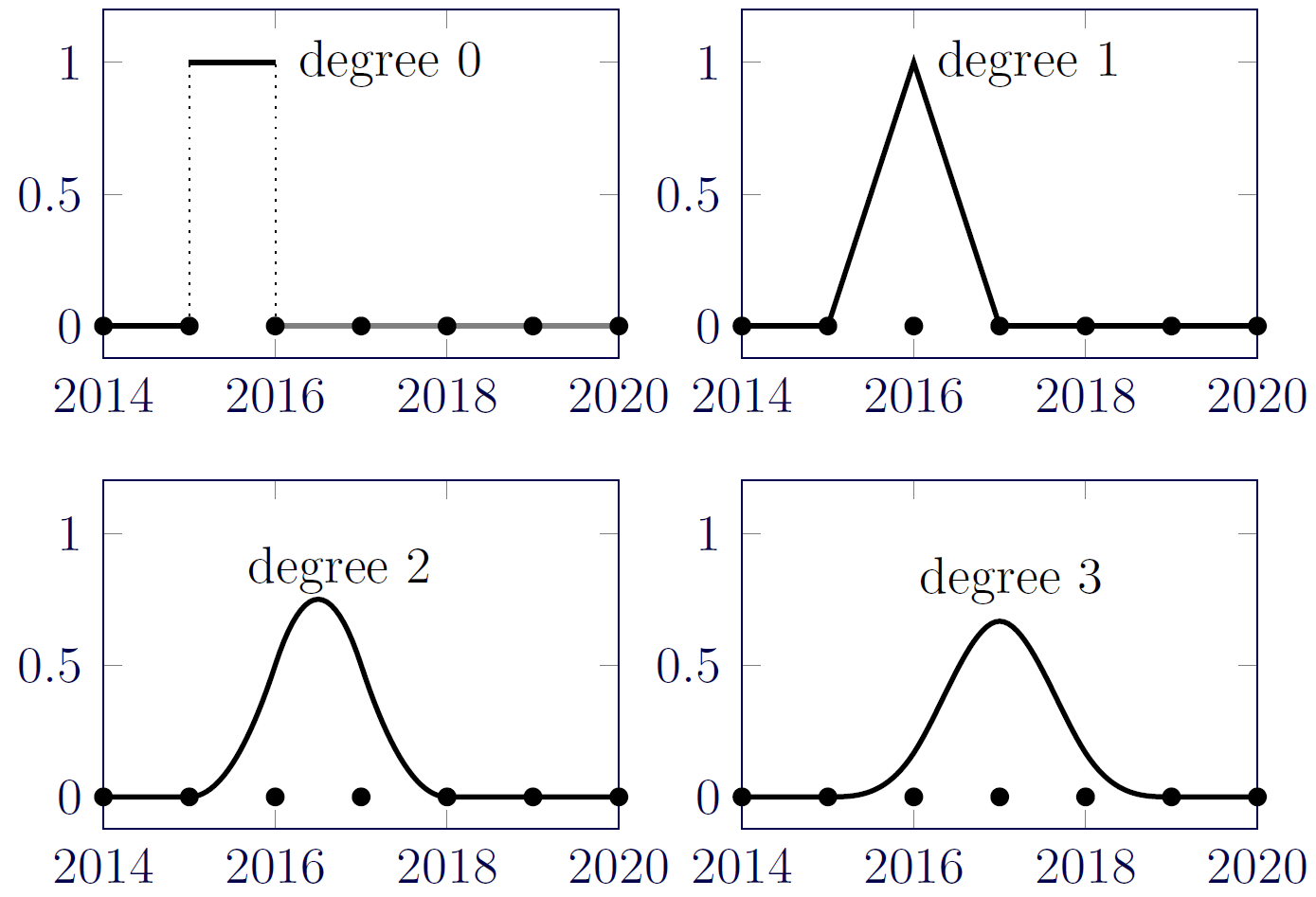
Figure 1 illustrates a number of properties of a single Schoenberg spline:

• The splines are local functions, and take the value zero outside their domain.
• The domain of a spline of degree $bdeg$ spans $bdeg+2$ knot points.
• The area under each spline is 1.

As Schoenberg splines are local functions, we need a basis of overlapping splines to span an interval.  An example is shown in Figure 2 for cubic splines, which is the most commonly used degree.  Such splines are referred to as "natural" cubic splines.

Figure 2. A basis of cubic Schoenberg (1964) splines spanning 2015–2020.

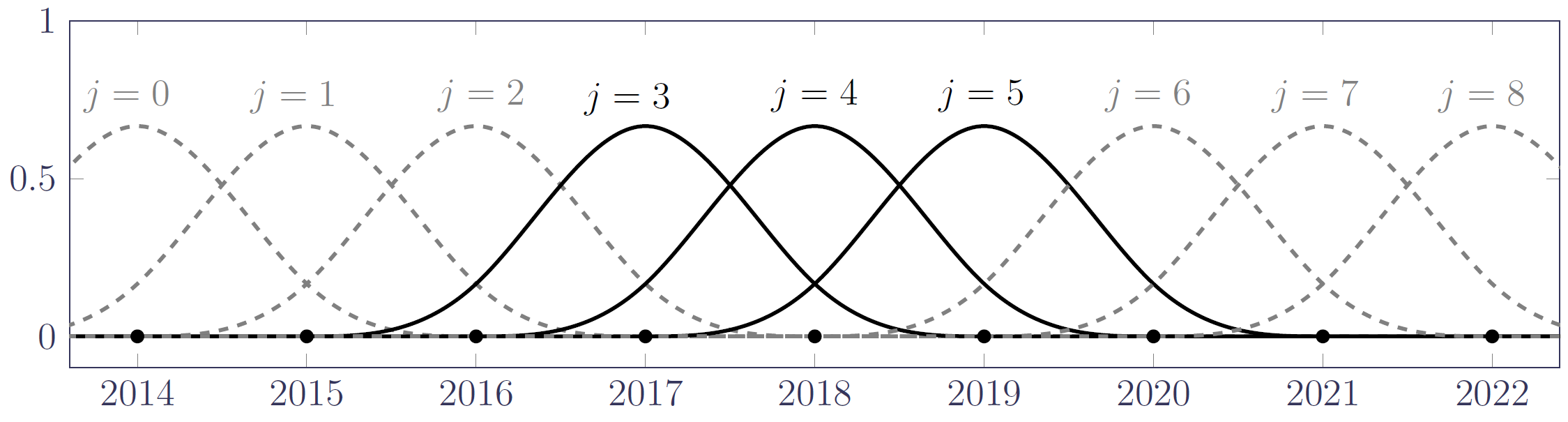
A collection of overlapping Schoenberg splines usually goes by the name of a $B$-spline basis. Such a basis has a number of additional properties:

• To span an interval there will be both splines wholly inside the interval and also splines only partly sitting in the interval.  In Figure 2 the former are drawn with solid black lines, while the latter edge splines are drawn with dashed grey lines.
• At any point within the interval there will be $bdeg+1$ splines with a non-zero value. These spline values will sum to 1.
• Outside the interval there are no such guarantees.

In Figures 1 & 2 the knot spacing is equidistant and set at one year.  However, neither is a necessary feature of splines:

• Currie, Durban & Eilers (2004) used a five-year knot spacing to model and forecast long-term trends in mortality rates.
• Richards (2021) used half-year knot spacing to model seasonal variation in mortality, and further used variable knot spacing to model the pandemic shock mortality of 2020 and 2021.

Further details of $B$-splines can be found in de Boor (2001). An introduction to their application in mortality modelling (with R code) can be found in Macdonald et al (2018).