A chill wind
In a previous blogs I have looked at seasonal fluctuations in mortality, usually with lower mortality in summer and higher mortality in winter. The subject of excess winter deaths is back in the news, as the UK experienced heavy mortality in the winter of 2014/15, as demonstrated in Figure 1.
Figure 1. Excess winter deaths in England & Wales. Source: ONS.
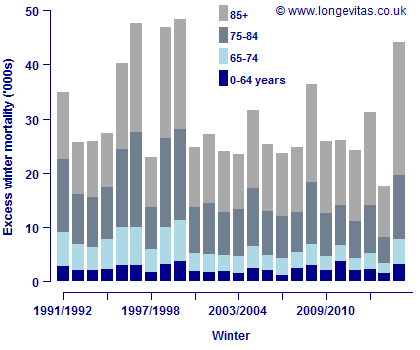
Figure 1 shows some important features, but some are less immediately obvious than others. The most obvious feature is that the winter of 2014/15 is indeed the worst for excess winter deaths for fifteen years. Another obvious feature of Figure 1 is that it is the elderly who bear the overwhelming brunt of excess winter mortality. However, there is an easily overlooked feature of Figure 1, namely that the winter of 2013/14 had the lowest excess winter mortality for over two decades. One is left wondering if the heavy mortality 2014/15 was partly due to frail individuals who managed to survive the winter of 2013/14? Another question is whether the generally lower level of excess winter deaths since the start of the Millennium is the result of public policy? Iparraguirre (2014) saw a "significant structural break in trend and volatility" around this time and found that winter fuel payments "can account for almost half of the reduction in EWM in England and Wales since 1999/2000". This would be an example of mortality plasticity, where changes in social policy can significantly reduce mortality levels.
In the accompanying bulletin released by the ONS, mention was made of the fact that "respiratory diseases were the underlying cause of death in more than a third of all excess winter deaths in 2014/15". The bulletin has a large section on influenza, which plays a big role in excess winter mortality and can disproportionately affect the elderly (this isn't always the case, however, as the influenza pandemic of 1918 showed). Since people of post-retirement age are usually the ones mainly affected by excess winter mortality, there are some important corollaries for actuaries working with pension schemes and annuity portfolios:
- Any experience analysis of a portfolio is best based on at least three contiguous years of data (say) if the results are not to be skewed by a year of abnormally heavy mortality. We have seen in a past blog that survival models are best-placed to model multi-year mortality for individuals.
- Any experience analysis of a portfolio should contain the same number of each season so that high winter mortality is balanced by lower summer mortality.
- For mortality forecasting, the recent fluctuations may have undue influence on the direction of the central projection. The impact of this will vary according to the structure of the mortality model, so it is particularly important to use multiple models and not rely on any single model.
References:
Iparraguirre, J. (2014), Have winter fuel payments reduced excess winter mortality in England and Wales?, Journal of Public Health (2014), doi: 10.1093/pubmed/fdu063.


Add new comment