Hedging or betting?
Last week I presented at Longevity 14 in Amsterdam. A recurring topic at this conference series is index-based approaches to managing longevity risk. Indeed, this topic crops up so reliably, one could call it a hardy perennial.
For a long time insurers and pension schemes were sceptical of derivatives-based solutions to managing longevity risk. Part of this scepticism was due to basis risk — why enter into a contract based on population mortality when a portfolio has very specific mortality characteristics? In particular, most portfolios tend to have a concentration of risk in a relatively small subset of lives. Another reason for scepticism was price — it was often cheaper to reinsure the entire risk of a portfolio, thus eliminating basis risk (sometimes called an indemnity solution to distinguish it from the partial risk transfer in a population-based solution). Why enter into a more-expensive contract that leaves you with basis risk when a cheaper solution transfers all the risk? For these and other reasons, population-based longevity derivatives didn't exactly set the heather alight.
However, in recent years a number of index-based hedges have been put in place by Dutch insurers; see Blake et al (2018) for an overview. For a detailed treatment of index-based hedging the reader can consult Cairns & Boukfaoui (2016), but the basic idea is this:
- The insurer and investor agree a contract where the payoff, \(h\), is based on the population mortality experience at a given date in the future, say \(n\) years away
- At that point a mortality projection is made, say by fitting a Lee-Carter model to the experience data. The model is used to calculate a commutation value to close out the contract.
- The commutation calculation should be useful for hedging the insurer's liabilities, e.g. an annuity factor at age \(x\). The hedge contract will specify other important items, e.g. the discount rate or yield curve to use.
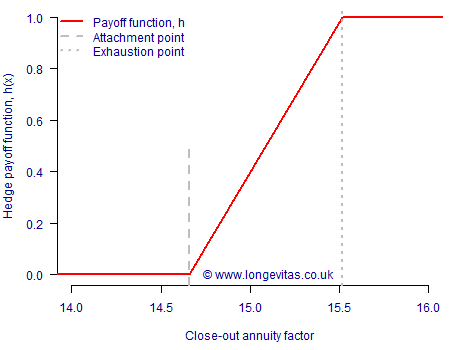
- The insurer only receives payment if the annuity factor exceeds an amount called the attachment point, \(A\).
- To limit the amount the investor has to pay, the annuity factor is subject to a maximum amount called the exhaustion point, \(E\).
The annuity factor in Stage 3 above is the unknown, so we can regard it as a random variable, \(X\). Without loss of generality we can scale the payoff so it ranges between zero and one, as per Cairns & El Boukfaoui (2016):
\[h(X)=\max\left(0,\min\left(\frac{X-A}{E-A},1\right)\right)\]
The shape of our hedge is shown in Figure 1:
Figure 1. Financial topiary – an example hedge payoff function.
For pricing we need to know the probability distribution of \(h(X)\), which clearly depends on the random variable \(X\). And how do we assess the distribution of \(X\)? The answer lies in noting that Steps 1–3 above are the same as the value-at-risk procedure proposed in our paper (Richards, Currie & Ritchie, 2014). There are three important variations:
- The term is \(n\) years instead of the single year used in the paper.
- The attachment and exhaustion points are set at different quantiles than the 99.5th used for Solvency II work.
- Although the model used to calculate the annuity factor for payoff is fixed, we do not necessarily have to use the same model to generate the mortality scenarios.
Cairns & Boukfaoui (2016) set their attachment point as the 60th percentile of \(X\) and their exhaustion point as the 95th percentile of \(X\), so we will do the same. To give ourselves a concrete example to work with, let's assume that the insurer or pension scheme has a portfolio of 55-year-old Dutch males with deferred annuities commencing payment at age 70. To hedge the insurer's liability we pick as a hedging instrument an annuity at age \(x=70\) with a term \(n=15\). For the sake of illustration we discount all cashflows at 2%, and we start by using the same smoothed Lee-Carter model for both mortality forecasts and annuity valuation. We use 5,000 simulations of the \(n\)-year value-at-risk procedure from Richards, Currie & Ritchie (2014) and find the following:
- The attachment point is the 60th percentile, i.e. 14.662.
- The exhaustion point is the 95th percentile, i.e. 15.520.
- The probability of a non-zero payoff is 0.40, being 1-0.60.
- The mean payoff of \(h(X)\) is 0.376.
So far, so good, and these attachment and exhaustion points could be written into the contract. However, regular readers of this blog will know how dangerous it is to rely on longevity forecasts from just one model. We therefore perform the same value-at-risk simulations using a number of alternative models for the experience over the following fifteen years (but using the same Lee-Carter model in Step 2 as the commutation calculation). For our investigation of model risk we use M5 and M6 from Cairns et al (2009) and the two-dimensional age-cohort (2DAC) P-spline model from Richards, Kirkby & Currie (2006).
Table 1. Hedge payoffs, \(h(X)\), using four different stochastic projection models for mortality rates for Dutch males. Source: own calculations using mortality data 1971–2016 for males in the Netherlands aged 50–104.
| Model for forecasting |
Probability of payoff |
Mean payoff |
|---|---|---|
| Lee-Carter | 0.40 | 0.376 |
| M5 | 0.53 | 0.592 |
| 2DAC | 0.80 | 0.434 |
| M6 | 0.82 | 0.710 |
Table 1 shows that the probability of a payout depends critically on the choice of model. Defining the attachment and exhaustion points with reference to the Lee-Carter forecasts risks understating the probability of payout by half if reality is like the M6 or 2DAC models. Of course, the converse is also true — if the roles were reversed the probability of payout could be dramatically overstated. Even when two models roughly agree on the payout probability, Table 1 also shows that there is variability in the mean payout – the 2DAC and M6 models have similar payout probabilities, but the average M6 payout is markedly larger.
When dealing with longevity derivatives we not only have caveat emptor, we have caveat venditor as well. Regardless of which side of a longevity derivative you sit, you always need to be aware of model risk.
References:
Blake, D., Cairns, A. J. G., Dowd, K. and Kessler, A. (2018) Still living with mortality: the longevity risk-transfer market after one decade. Presented at a Sessional Research Meeting of the Institute and Faculty of Actuaries, Edinburgh, 29 January, 2018. British Actuarial Journal (to appear).
Cairns, A. J. G., Blake, D., Dowd, K., Coughlan, G. D., Epstein, D., Ong, A. and Balevich, I. (2009) A quantitative comparison of stochastic mortality models using data from England and Wales and the United States, North American Actuarial Journal, 13(1), pages 1–35.
Cairns, A. J. G. and El Boukfaoui, G. (2016) Basis Risk in Index-Based Longevity Hedges: A Guide for Longevity Hedgers, North American Actuarial Journal (to appear).
Richards, S. J. , Kirkby, J. G. and Currie, I. D. (2006) The importance of year of birth in two-dimensional mortality patterns, British Actuarial Journal, 12(I), pages 5–61.
Richards, S. J., Currie, I. D. and Ritchie, G. P. (2014) A value-at-risk framework for longevity trend risk, British Actuarial Journal, 19(1), pages 116–167.
Previous posts
'D' is for deficiency
Smooth Models Meet Lumpy Data
Most of the survival models used by actuaries are smooth or piecewise smooth; think of a Gompertz model for the hazard rate, or constant hazard rates at individual ages. When we need a cumulative quantity, we use an integral, as in the cumulative hazard function, \(\Lambda_x(t)\):
\[ \Lambda_x(t) = \int_0^t \mu_{x+s} \, ds. \qquad (1) \]


Add new comment