Between the lines

Actuaries make great use of so-called standard tables.  These are annual probabilities at each whole age for males and females.  However, often mortality rates are required at ages which are not whole numbers.  Since the rates in standard tables change relatively smoothly from one age to the next, a natural approach is to use interpolation to approximate the rates between whole ages.

The simplest approach is linear interpolation, which uses the rates at ages on either side of the target age.  However, this suffers from the drawback that mortality rates at post-retirement ages increase exponentially with age.  The consequence of this is that linearly interpolated rates are always too high and will thus slightly under-estimate annuity reserves.  This is illustrated in Figure 1, which uses the mortality rates at ages 70 and 72 to interpolate the rate at age 71.  Since we actually know the mortality rate at age 71, this gives us the ability to evaluate the accuracy of the interpolation method.

Figure 1. Interpolation of mortality rates between ages 70 and 72. Source: Own calculations using male rates from S1PA.

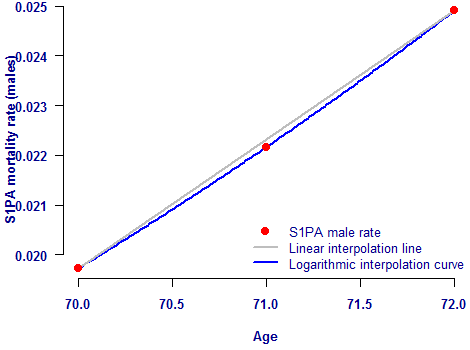
Since mortality rates usually increase exponentially, the logarithm of the mortality rates is therefore linear (or close to it). This means that linear interpolation using log q_x will be more accurate than linear interpolation using q_x directly. This is demonstrated by the second line in Figure 1, which shows that logarithmic interpolation of mortality rates produces more accurate approximations at post-retirement ages.