Mortality convergence
In his blog on socio-economic differentials in England and Wales, Torsten Kleinow showed how mortality rates between sub-groups converge with age. And in his blog on ill-health retirements, Kai Kaufhold demonstrated how excess mortality relative to normal retirements reduces, then vanishes. Both are examples of the phenomenon known to demographers as the compensation law of mortality — regardless of the initial differentials between two contemporaneous sub-populations, their mortality rates will converge at an advanced age, often around 90–95.
[We will caveat this for casual readers by stating that we are talking about human populations in peacetime, where external causes of death such as accident or murder are relatively unimportant at post-retirement ages. Note also that the compensation law of mortality discussed here is different from the sort of convergence in rates seen after the reunification of the two Germanies in 1990, which is regarded as an example of mortality plasticity].
Gender is a special case for mortality convergence — while different sub-groups of males will converge on the same mortality rates at advanced ages, sub-groups of females will converge on a different (lower) female rate. Male-female differentials also narrow with increasing age, but they do not disappear entirely as they do with other risk factors. This is ideally allowed for in mortality modelling, as shown in Figure 1:
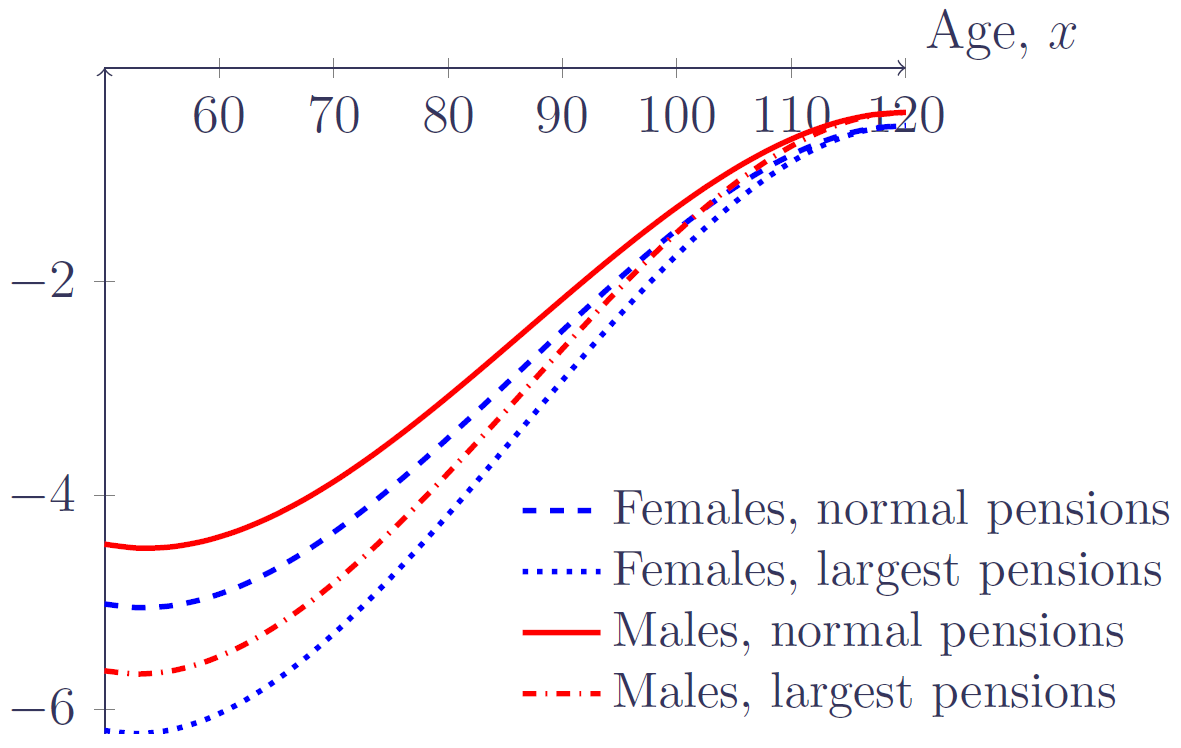
Figure 1. Modelled mortality hazard (log scale) for males and females by pension size-band. Source: Richards (2019).
The phenomenon of mortality convergence is of considerable interest to actuaries:
The rate of convergence is directly linked to the size of the initial differential. The larger the initial difference between two sub-groups, the faster the rate of convergence will be. In Torsten's blog on socio-economic differences, the larger the difference between two groups at age 40, the greater the difference in slope as the mortality rates converge somewhere in the 90–95 age range.
The impact of converging mortality rates can be further amplified by discounting cashflows. Discounting puts less weight on cashflows further into the future, thus magnifying the financial impact of near-term mortality differentials.
It is insufficient to allow for mortality differentials just by using a different (flat) percentage of a mortality table. While it might be a handy shorthand to say that a sub-group has mortality z%z% higher (or lower) than a reference group, this is only a crude approximation. In practice, the mortality excess would be higher than z%z% at younger ages, decreasing to essentially zero at around age 95 or so. As a portfolio ages, therefore, the mortality differentials will reduce. This is particularly important in valuating annuities in payment, as a failure to allow for reducing excess mortality can lead to premature release of reserves. This is a particular risk for portfolios of impaired-life annuities.
References:
Richards, S. J. (2019) A Hermite-spline model of post-retirement mortality, Scandinavian Actuarial Journal, DOI: 10.1080/03461238.2019.1642239.
Previous posts
Auditing firewalls
Fun and games with constraints
I'm a statistician so I worry about standard errors just as much as I worry about point estimates. My blog Up close and intimate with the APCI model looked at the effect of different constraints on parameter estimates in models of mortality. This blog looks at the effect of constraints on the standard errors of the parameter estimates.


Add new comment