Run-off volatility

When investigating risk in an annuity portfolio, a key task is to simulate the future lifetime for each annuitant.  Survival models make this particularly easy, as covered in an earlier posting on simulating lifetimes.

One of the first things which strikes practitioners is that volatility in run-off valuations increases with the average age of a portfolio.  The reason for this is that the variation in future lifetime gets larger relative to the average future lifetime.  One way of looking at this is to use the coefficient of variation, which is simply the standard error of the future lifetime divided by the mean:

coefficient of variation = standard error / mean

The coefficient of variation is normalised in that it expresses variability relative to the mean.  It is therefore sometimes expressed as a percentage to show relative volatility.  This is illustrated in Figure 1, which shows the distribution of age at death by duration since outset for three key ages.

Figure 1. Distribution of age at death by time since outset.  Mortality according to S1PA males.

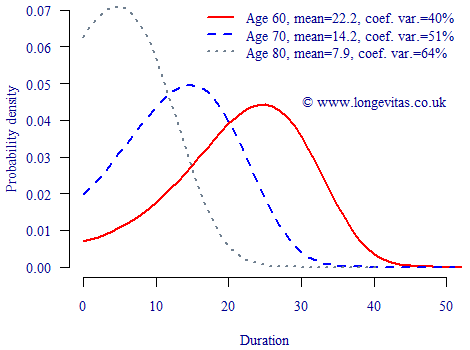
Figure 1 shows that the actual variation in future lifetime is largest for younger ages, as indicated by the wider spread. However, when this variation is expressed relative to the expected future lifetimes, we see that the relative volatility is actually larger at older ages. A corollary of this is that pensions or annuities with spouses' benefits will lower the relative volatility in run-off, in part because spouses' benefits increase the average duration of payments.