Robust mortality forecasting for multivariate models

In my previous blog I showed how univariate stochastic mortality models, like the Lee-Carter and APC models, can be robustified to cope with data affected by the covid-19 pandemic.  Such robustification is necessary because outliers, such as the 2020 experience, bias parameter estimates and affect value-at-risk (VaR) capital requirements.  Kleinow & Richards (2016) showed how one-year VaR-style capital requirements are heavily dependent on the variance of the error process, which is inflated by the presence of outliers.

However, there is an important class of mortality models that is not univariate: the Cairns-Blake-Dowd (CBD) family.  There are numerous members of this family, but here we will focus on M9 (Cairns et al, 2015).  Under M9 the mortality hazard, \(\mu_{x,y}\), at age \(x\) in year \(y\) is modelled as follows:

\[\log\mu_{x,y} = \alpha_x + \kappa_{0,y}+\kappa_{1,y}S(x)+\kappa_{2,y}Q(x)+\gamma_{y-x}\]

where \(S(x)=x-{\bar x}\), \(Q(x)=(x-{\bar x})^2-\hat\sigma^2\) and \(\hat\sigma^2=\frac{1}{n_x}\sum_i (x_i-\bar x)^2\), with \(n_x\) being the number of distinct ages \(\{x_1,x_2,\ldots,x_{n_x}\}\).  For simplicity we denote \(\boldsymbol{\kappa}=(\kappa_0, \kappa_1, \kappa_2)\).

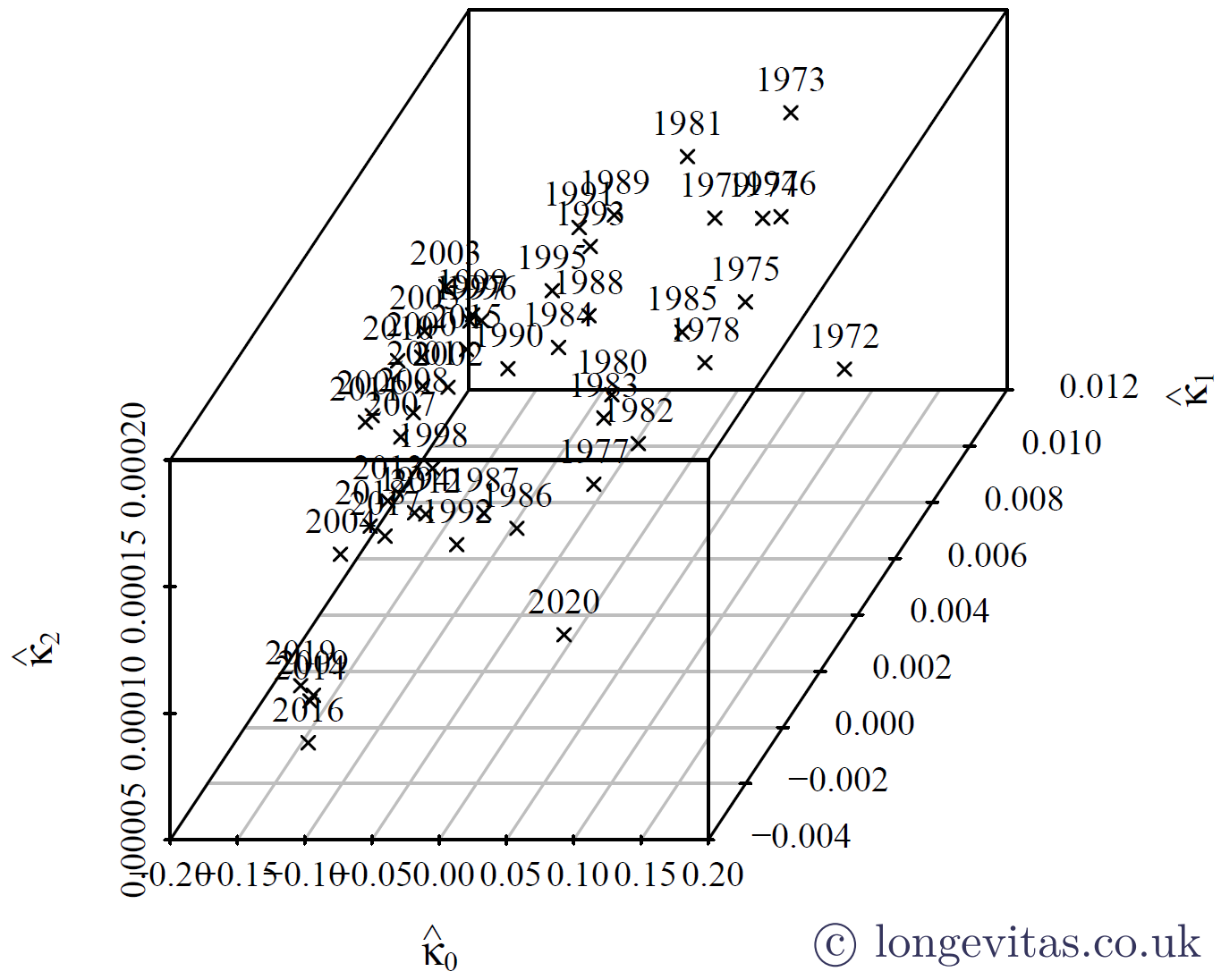
M9 forecasts mortality assuming that \(\boldsymbol{\kappa}\) follows a trivariate random walk with drift.  Outliers in multivariate data are sometimes tricky to see visually; Figure 1 shows that the 2020 mortality experience is not obviously anomalous, despite knowing that the data are affected by a global pandemic.

Figure 1. Pseudo-3D parameter plot for M9. Source: own calculations using HMD data for males in England & Wales, ages 50–105.

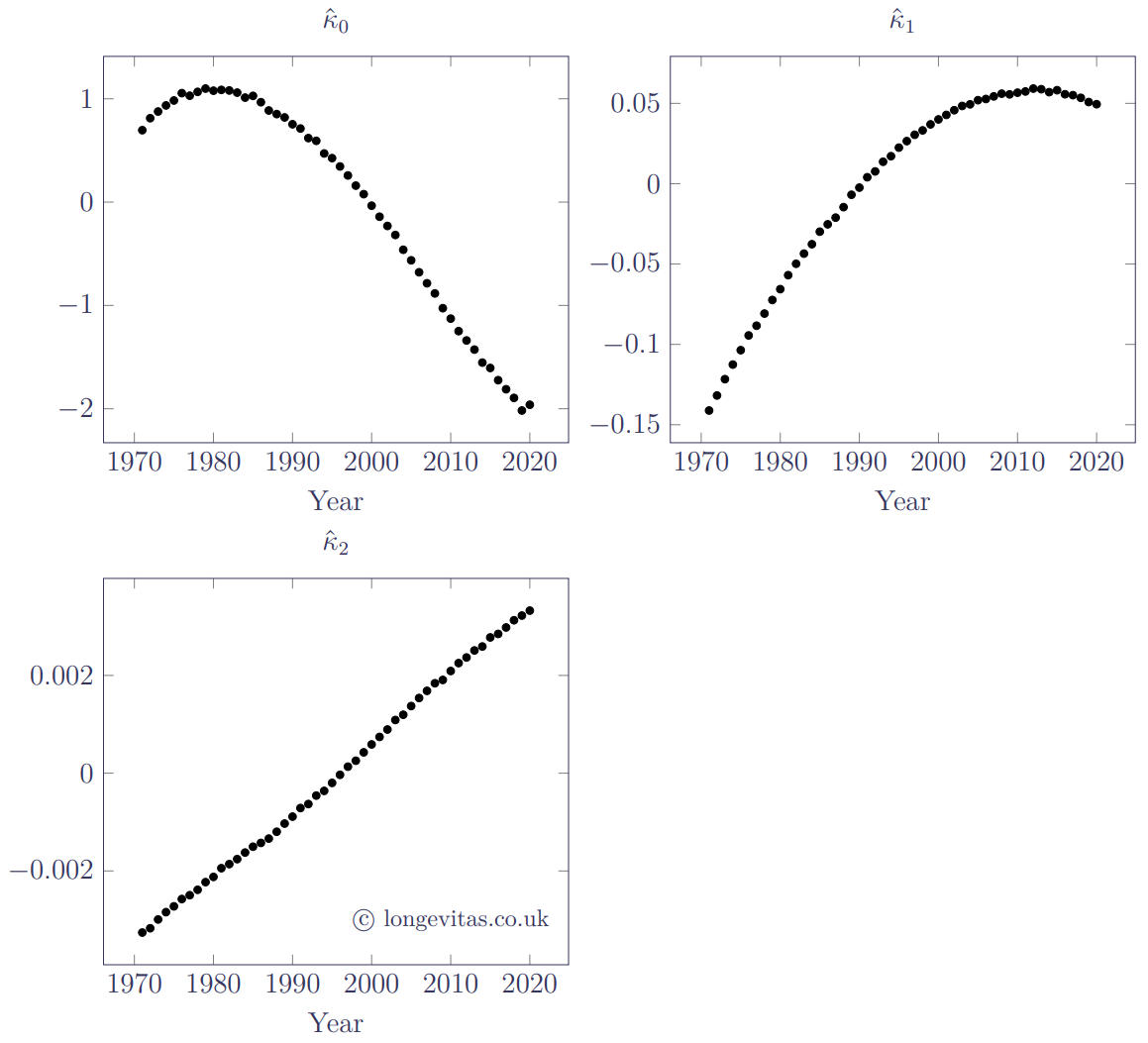
The situation is no easier when plotting the parameter series individually, as shown in Figure 2.

Figure 2.  Parameter plots for M9. Source: own calculations using HMD data for males in England & Wales, ages 50–105.

However, the core CBD projection assumption is that the \(\boldsymbol{\kappa}\) terms follow a multivariate random walk with drift. This means that the first differences follow a multivariate normal distribution with constant mean vector \(\boldsymbol{\mu}\) and covariance matrix \(\boldsymbol{\Sigma}\).  For a given observation, \(\boldsymbol{x}\), this allows us to calculate the Mahalanobis distance, \(D\), as follows:

\[D=\sqrt{(\boldsymbol{x}-\boldsymbol{\mu})^T\boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})}\]

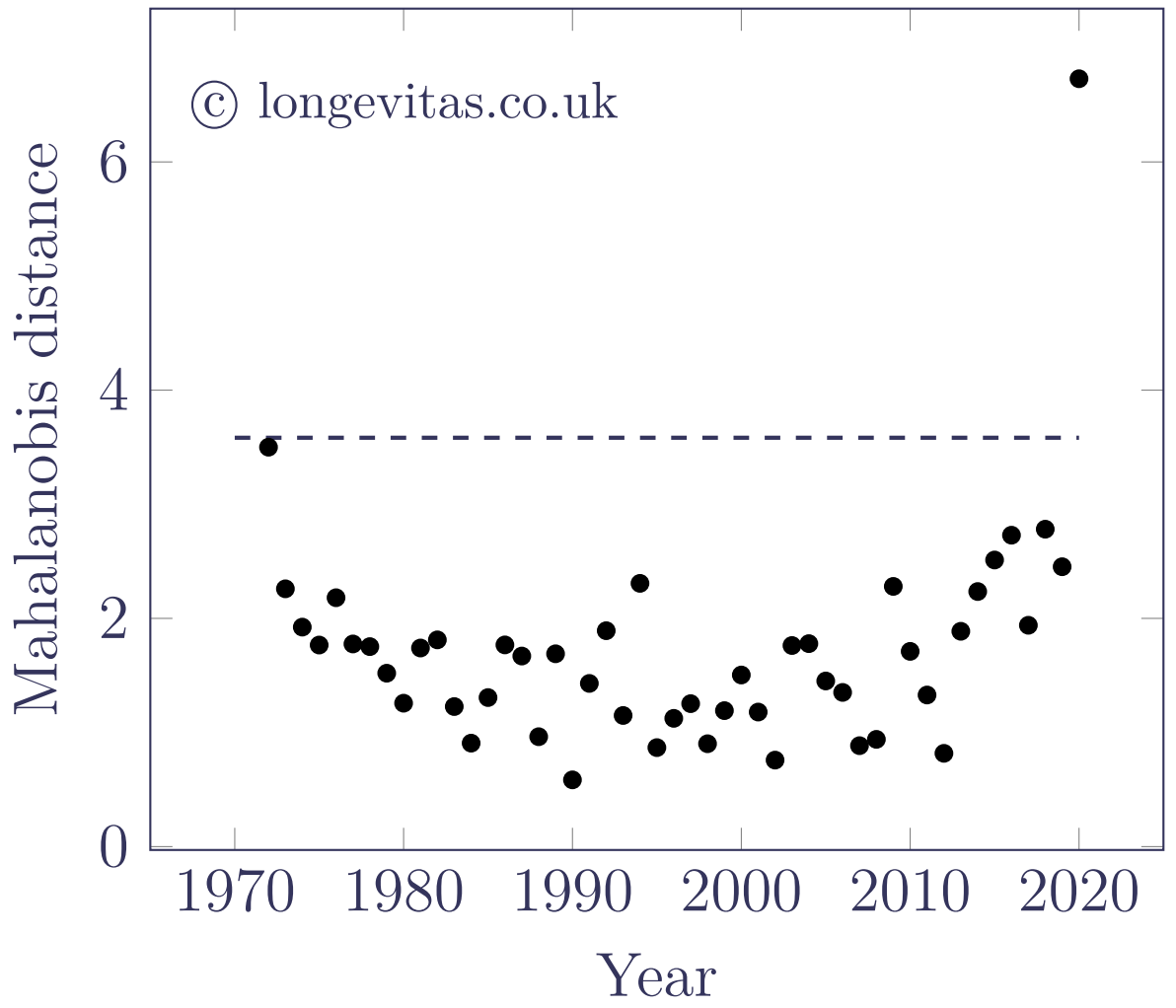
The Mahalanobis distance reduces a \(p\)-dimensional observation, \(\boldsymbol{x}\), into a scalar measure, as shown in Figure 3.

Figure 3. Mahalanobis distance, \(D\), for first differences of \(\boldsymbol{\kappa}\) for M9.  Source: own calculations using HMD data for males in England & Wales, ages 50–105.

Using the Mahalanobis distance, we can test the size of a potential outlier using the following assumption:

\[D^2\sim \chi^2_{p}\]

where \(p=2\) for M5 and M6 and \(p=3\) for M7 and M9.  Outliers can be detected by comparing \(D^2\) against a suitable threshold from the \(\chi^2_p\) distribution (the dashed line in Figure 2 is the square root of the upper \(\alpha=0.5\%\) point of the \(\chi^2_3\) distribution function).  Thus, for a multivariate random walk with drift we can use the Mahalanobis distance to identify outliers amount the first differences.

Alternatively, we can robustify the series directly.  For example, Galeano, Peña & Tsay (2006) extended the univariate outlier-detection approach of Chen & Liu (1993) for ARIMA models to vector-ARIMA (VARMA) models.  A multivariate random walk with drift is a special case of a VARMA model.

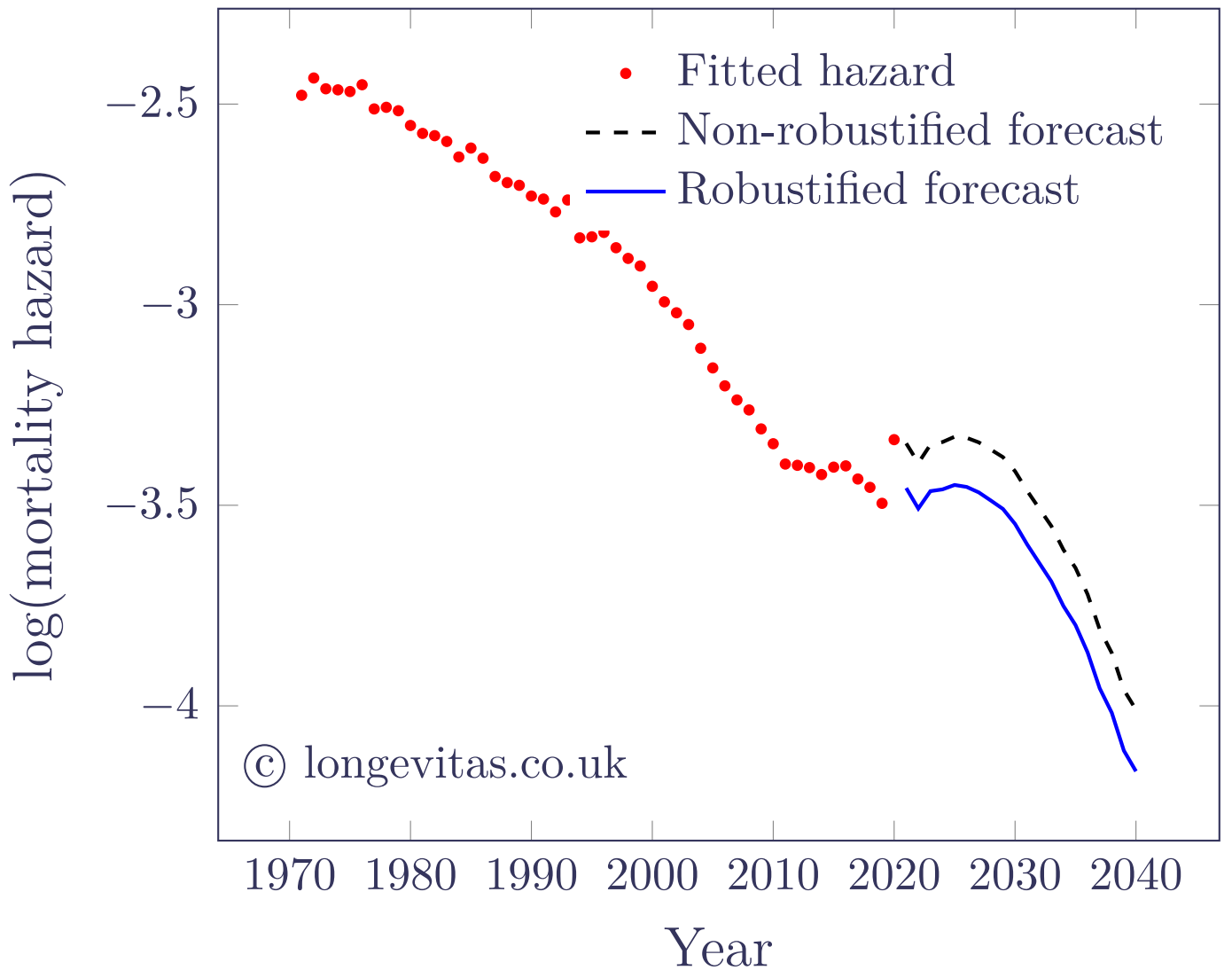
Figure 4 shows an example of robustification of M9 using the approach of Galeano, Peña & Tsay (2006).  As in the univariate case, the outliers are identified and the outlier effects are co-estimated along with the model parameters.  This yields not only robust parameter estimates, but also permits the calculation of a robust starting point for the forecast from 2020.

Figure 4. Estimated and forecast values of log(mortality hazard) at age 70 for M9 model of mortality for males in England & Wales. Robustified model fitted using undifferenced series and methodology of Galeano, Peña & Tsay (2006) with critical value of \(\alpha=0.5\%\).